Assignment 1#
Dave Friedman
CMPSC 465 Data Structures and Algorithms
Summer 2024
Table of Contents#
Auxiliary Code#
Show code cell source
import numpy as np
from scipy.special import factorial
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.style.use('ggplot');
plt.rcParams.update({'text.usetex' : True});
%matplotlib inline
Problem 1 - Big Oh#
1A#
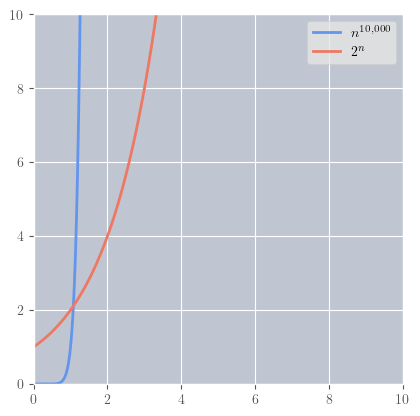
\( \begin{aligned} f(n) &= n^{10000} \\ g(n) &= 2^n \\ \end {aligned} \)
\( \begin{aligned} \lim_{n \to \infty} \frac{f(n)}{g(n)} = \lim_{n \to \infty} \frac{n^{10000}}{2^n} \end {aligned} \)
One application of L’Hospital’s rule yields:
\( \begin{aligned} \lim_{n \to \infty} \frac{10,000 \cdot n^{9999}}{\ln 2 \cdot 2^n} = \frac{10,000}{\ln 2} \lim_{n \to \infty} \frac{n^{9999}}{2^n} \end {aligned} \)
Ten thousand applications of L’Hospital’s rule yields:
\( \begin{aligned} \left( \frac{10,000}{\ln 2} \times \frac{9,999}{\ln 2} \times \dots \times \frac{2}{\ln 2} \times \frac{1}{\ln 2} \right) \lim_{n \to \infty} \frac{1}{2^n} = \left( \frac{10,000!}{\ln^{10,000} 2} \right) \lim_{n \to \infty} \frac{1}{2^n} \end {aligned} \)
The factor \(\begin{aligned} \frac{10,000!}{\ln^{10,000} 2} \end{aligned}\) is just a constant and \(\begin{aligned} \lim_{n \to \infty} \frac{1}{2^n} \end{aligned} = 0\) and so
\( \begin{aligned} \lim_{n \to \infty} \frac{f(n)}{g(n)} = \lim_{n \to \infty} \frac{n^{10000}}{2^n} = 0 \end {aligned} \)
Therefore
\(f = o(g) \implies f = O(g)\)
where the antecedent states that function \(f\) grows slower than a constant multiple of function \(g\) for all sufficiently large \(n\)
and the consequent states that function \(f\) grows no faster than a constant multiple of function \(g\) for all sufficiently large \(n\)
Show code cell source
s = 10
n = np.linspace(0, s, 1001)
f = n**10 # n = 10,000
g = 2**n
fig = plt.figure();
ax = plt.subplot();
ax.set_aspect(1);
ax.plot(n, f, label='$n^{10,000}$', linewidth=2, color='#6495ED');
ax.plot(n, g, label='$2^n$', linewidth=2, color='#ED7864');
ax.set_facecolor('#c0c6d1')
ax.set_xlim(0,s);
ax.set_ylim(0,s);
ax.legend();
1B#
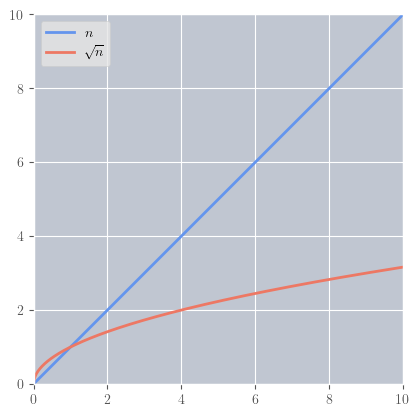
\( \begin{aligned} f(n) &= n \\ g(n) &= \sqrt{n} \\ \end {aligned} \)
\( \begin{aligned} \lim_{n \to \infty} \frac{f(n)}{g(n)} = \lim_{n \to \infty} \frac{n}{\sqrt{n}} = \lim_{n \to \infty} (n^{\frac{1}{2}}) = \left( \lim_{n \to \infty} n \right)^{\frac{1}{2}} = \infty \end {aligned} \)
Therefore
\(f = \omega(g) \implies f = \Omega(g)\)
where the antecedent states that function \(f\) grows faster than a constant multiple of function \(g\) for all sufficiently large \(n\)
and the consequent states that function \(f\) grows no slower than a constant multiple of function \(g\) for all sufficiently large \(n\)
Show code cell source
s = 10
n = np.linspace(0, s, 1001)
f = n
g = n**0.5
fig = plt.figure();
ax = plt.subplot();
ax.set_aspect(1);
ax.plot(n, f, label='$n$', linewidth=2, color='#6495ED');
ax.plot(n, g, label='$\sqrt{n}$', linewidth=2, color='#ED7864');
ax.set_facecolor('#c0c6d1')
ax.set_xlim(0,s);
ax.set_ylim(0,s);
ax.legend();
1C#
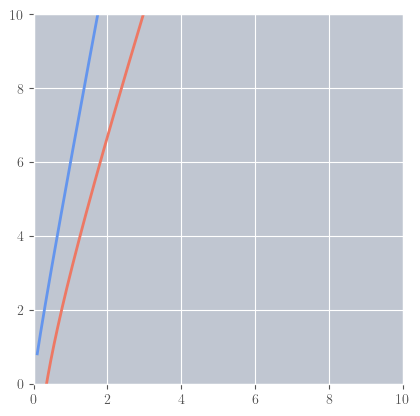
\( \begin{aligned} f(n) &= 5n + \sqrt{n} \\ g(n) &= 3n + \log n \\ \end {aligned} \)
\( \begin{aligned} \lim_{n \to \infty} \frac{f(n)}{g(n)} = \lim_{n \to \infty} \frac{5n + \sqrt{n}}{3n + \log n} = \lim_{n \to \infty} \frac{5 + \frac{1}{n^{\frac{1}{2}}}}{3 + \frac{\log n}{n}} = \frac{5 + \lim_{n \to \infty} \frac{1}{n^{\frac{1}{2}}}}{3 + \lim_{n \to \infty} \frac{\log n}{n}} \end {aligned} \)
\( \begin{aligned} \lim_{n \to \infty} \frac{\log n}{n} \overset{\text{L'Hospital}}{=} \lim_{n \to \infty} \frac{\frac{1}{n}}{1} = \lim_{n \to \infty} \frac{1}{n} = 0 \end {aligned} \)
\( \begin{aligned} \frac{5 + \lim_{n \to \infty} \frac{1}{n^{\frac{1}{2}}}}{3 + \lim_{n \to \infty} \frac{\log n}{n}} = \frac{5}{3} \end {aligned} \)
Therefore
\(f = \Theta(g)\)
function \(f\) grows at the same rate as a constant multiple of function \(g\) for all sufficiently large \(n\)
Show code cell source
s = 10
n = np.linspace(0.1, s, 1001)
f = 5*n + np.sqrt(n)
g = 3*n + np.log(n)
fig = plt.figure();
ax = plt.subplot();
ax.set_aspect(1);
ax.plot(n, f, label='', linewidth=2, color='#6495ED');
ax.plot(n, g, label='', linewidth=2, color='#ED7864');
ax.set_facecolor('#c0c6d1')
ax.set_xlim(0,s);
ax.set_ylim(0,s);
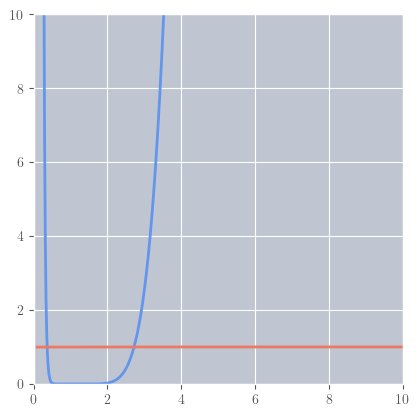
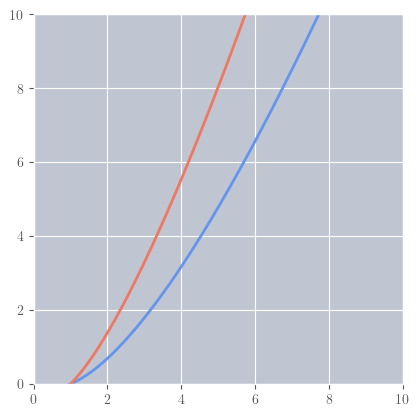
1D#
\( \begin{aligned} f(n) &= \log (n!) \\ g(n) &= n \log n \\ \end {aligned} \)
\( \begin{aligned} \log (n!) &= \log (n \times n - 1 \times \dots \times 2 \times 1) &&= \log (n) && + && \log (n - 1) && + && \dots && + && \log (2) && + && \log (1) \\ n \log n & &&= \log (n) && + && \log (n) && + && \dots && + && \log (n) && + && \log (n) \\ \end {aligned} \)
Therefore the limit has an upper bound of \(1\):
\(\log (n!) \le n \log n \implies \frac{\log (n!)}{n \log n} \le 1\)
How to show a lower bound of \(1\)?
https://math.stackexchange.com/questions/376988/limit-of-frac-lognn-logn-as-n-to-infty
\( \begin{aligned} \lim_{n \to \infty} \frac{f(n)}{g(n)} = \lim_{n \to \infty} \frac{\log (n!)}{n \log n} = 1 \end {aligned} \)
Therefore
\(f \sim g \implies f = \Theta(g)\)
not only does function \(f\) grow at the same rate as a constant multiple of function \(g\) for all sufficiently large \(n\) but \(\frac{f}{g}\) approaches \(1\)
Show code cell source
s = 10
n = np.linspace(0.1, s, 1001)
f = np.log(factorial(n))
g = n * np.log(n)
fig = plt.figure();
ax = plt.subplot();
ax.set_aspect(1);
ax.plot(n, f, label='', linewidth=2, color='#6495ED');
ax.plot(n, g, label='', linewidth=2, color='#ED7864');
ax.set_facecolor('#c0c6d1')
ax.set_xlim(0,s);
ax.set_ylim(0,s);
1E#
\( \begin{aligned} f(n) &= \log^{100} n \\ g(n) &= n^{.001} \\ \end {aligned} \)
\( \begin{aligned} \lim_{n \to \infty} \frac{f(n)}{g(n)} = \lim_{n \to \infty} \frac{\log^{100} n}{n^{.001}} \end {aligned} \)
One application of L’Hospital’s rule yields:
\( \begin{aligned} \lim_{n \to \infty} \frac{100 \frac{1}{n} \cdot \log^{99} n}{\frac{1}{1000} \cdot \frac{1}{n^\frac{999}{1000}}} = 100 \times 1,000 \lim_{n \to \infty} \frac{\frac{1}{n} \cdot \log^{99} n}{\frac{1}{n^\frac{999}{1000}}} = 100 \times 1,000 \lim_{n \to \infty} \frac{\log^{99} n}{n^{.001}} \end {aligned} \)
One hundred applications of L’Hospital’s rule yields:
\( \begin{aligned} (100 \times 1,000) \times (99 \times 1,000) \times \dots \times (2 \times 1,000) \times (1 \times 1,000) \times \lim_{n \to \infty} \frac{\frac{1}{n}}{n^{.001}} = (100! \times 1,000^{100}) \times \lim_{n \to \infty} \frac{1}{n^{1.001}} \end {aligned} \)
The factor \(\begin{aligned} 100! \times 1,000^{100} \end{aligned}\) is just a constant and \(\begin{aligned} \lim_{n \to \infty} \frac{1}{n^{1.001}} \end{aligned} = 0\) and so
\( \begin{aligned} \lim_{n \to \infty} \frac{f(n)}{g(n)} = \lim_{n \to \infty} \frac{\log^{100} n}{n^{.001}} = 0 \end {aligned} \)
Therefore
\(f = o(g) \implies f = O(g)\)
where the antecedent states that function \(f\) grows slower than a constant multiple of function \(g\) for all sufficiently large \(n\)
and the consequent states that function \(f\) grows no faster than a constant multiple of function \(g\) for all sufficiently large \(n\)
Show code cell source
s = 10
n = np.linspace(0.1, s, 1001)
f = np.log(n)**10
g = n**(0.001)
fig = plt.figure();
ax = plt.subplot();
ax.set_aspect(1);
ax.plot(n, f, label='', linewidth=2, color='#6495ED');
ax.plot(n, g, label='', linewidth=2, color='#ED7864');
ax.set_facecolor('#c0c6d1')
ax.set_xlim(0,s);
ax.set_ylim(0,s);