Exercises#
FCCT 1990 Hill, Raymond. A First Course in Coding Theory. Clarendon Press: Oxford Applied Mathematics and Computing Science Series.
Programming Environment#
Show code cell source
# %load imports.py
import numpy as np
import pandas as pd
import matplotlib as mpl
from matplotlib.patches import Rectangle
import matplotlib.pyplot as plt
plt.style.use('ggplot');
plt.rcParams.update({'text.usetex' : True});
%matplotlib inline
from collections import defaultdict
from itertools import combinations,product
import itertools
from typing import Set
from IPython.display import display, Math
from datetime import datetime as d
import locale as l
import platform as p
import sys as s
pad = 20
print(f"{'Executed'.upper():<{pad}}: {d.now()}")
print()
print(f"{'Platform' :<{pad}}: "
f"{p.mac_ver()[0]} | "
f"{p.system()} | "
f"{p.release()} | "
f"{p.machine()}")
print(f"{'' :<{pad}}: {l.getpreferredencoding()}")
print()
print(f"{'Python' :<{pad}}: {s.version}")
print(f"{'' :<{pad}}: {s.version_info}")
print(f"{'' :<{pad}}: {p.python_implementation()}")
print()
print(f"{'Matplotlib' :<{pad}}: {mpl.__version__}")
print(f"{'NumPy' :<{pad}}: {np .__version__}")
#==================================================
def rc (q : int,
n : int) -> Set[str]:
"""Repetition Code
Generate a q-ary repetition block code of length n.
"""
S=set()
for i in range(q):
S.add(str(i)*n)
return S
def fqn (q : int,
n : int,
g : int = 0) -> Set[str]:
"""Construct a linear space of dimension n over a finite field of order q.
Parameters
==========
g : If the space is very large, opt for the first g elements of a generator object.
"""
if bool(g):
f=itertools.product(range(q),repeat=n)
return set(''.join(str(i) for i in next(f)) for _ in range(g))
else:
return {''.join(str(bit) for bit in word) for word in itertools.product(range(q),repeat=n)}
def qarycode_to_nbitstring (code={'3121','2101'},k=4):
"""Convert a q-ary code """
for n in code:
print(' '.join(format(int(i),f'0{k}b') for i in n))
def hd (a : str = '1001',
b : str = '0101') -> int:
"""HAMMING DISTANCE
Parameters
==========
x : str
y : str
Return
======
int
"""
assert len(a) == len(b), 'x and y must have the same length'
return sum(x!=y for x,y in zip(a,b))
def nbfmd (c : Set[str],
pr : bool = False) -> np.float16:
"""NAIVE BRUTE FORCE MINIMUM DISTANCE d(C)
Computes the pairwise Hamming distance for all codewords and returns the minimum value.
This is a naive (i.e., non vectorized) implementation using nested for loops.
Parameters
==========
c : code
pr : Print intermediate steps.
Returns
=======
d(C)
"""
# convert a set of string vectors to a 2D NumPy array of integers
c=np.array([list(codeword) for codeword in c],dtype=np.float16)
# intialize empty hamming distance matrix
hamming = np.empty([c.shape[0]]*2,dtype=np.float16)
for i,x in enumerate(c):
for j,y in enumerate(c):
hamming[i,j]=(x!=y).sum()
# the diagonal represents the Hamming distance of a codeword with itself, which is always 0.
np.fill_diagonal(hamming,np.inf)
if pr == True:
print(hamming)
return hamming.min().astype(np.int8)
def one_error_detecting (q : int,
code : Set[str],
p : bool = False) -> bool:
"""Verify that a code is one-error detecting.
No one-bit error equals a codeword.
"""
flag=True
alphabet=set(str(i) for i in range(q))
for codeword in code:
if p:
print()
print(f"{'orig cw : ':10}{codeword}")
for i in range(len(codeword)):
a,b,c=codeword[:i],codeword[i],codeword[i+1:]
symbols=alphabet-set(codeword[i])
for symbol in symbols:
cw=codeword[:i]+symbol+codeword[i+1:] # SINGLE ERROR
if cw in code:
flag=False
if p:
print(f"{'ERROR':10}{cw}")
else:
if p:
print(f"{'':10}{cw}")
return flag
# set(''.join(l for l in i) for i in itertools.product('10',repeat=3))
# set(''.join(l for l in i) for i in itertools.combinations_with_replacement('012',r=3))
# set(''.join(l for l in i) for i in itertools.combinations('01',r=2))
EXECUTED : 2025-01-17 19:46:27.995738
Platform : 15.2 | Darwin | 24.2.0 | arm64
: UTF-8
Python : 3.11.11 | packaged by conda-forge | (main, Dec 5 2024, 14:21:42) [Clang 18.1.8 ]
: sys.version_info(major=3, minor=11, micro=11, releaselevel='final', serial=0)
: CPython
Matplotlib : 3.9.3
NumPy : 2.0.2
1#
[1.1]#
If the following message were received from outer space, why might it be conjectured that it was sent by a race of human-like beings who have one arm twice as long as the other?
[Hint: The number of digits in the message is the product of two prime numbers.]
message='00110000011000111111110110010011001001100101111000100100010010001001001100110'
message
'00110000011000111111110110010011001001100101111000100100010010001001001100110'
len(message)
77
c=np.array(list(message)).reshape(11,7)
c
array([['0', '0', '1', '1', '0', '0', '0'],
['0', '0', '1', '1', '0', '0', '0'],
['1', '1', '1', '1', '1', '1', '1'],
['1', '0', '1', '1', '0', '0', '1'],
['0', '0', '1', '1', '0', '0', '1'],
['0', '0', '1', '1', '0', '0', '1'],
['0', '1', '1', '1', '1', '0', '0'],
['0', '1', '0', '0', '1', '0', '0'],
['0', '1', '0', '0', '1', '0', '0'],
['0', '1', '0', '0', '1', '0', '0'],
['1', '1', '0', '0', '1', '1', '0']], dtype='<U1')
print(np.array([[''.join(row)] for row in np.array(list(message)).reshape(11,7)]))
fig = plt.figure(figsize=(6,6));
ax = plt.subplot();
for i,row in enumerate(c):
for j,col in enumerate(row):
#print(i,j,col)
if int(col):
ax.add_patch(Rectangle((j,i),1,1,facecolor='blue'));
ax.set_aspect(1);
ax.set_xticks(ticks=np.arange(0,c.shape[1]+1));
ax.set_yticks(ticks=np.arange(0,c.shape[0]+1));
ax.set_xlim(0,c.shape[1]);
ax.set_ylim(c.shape[0],0);
[['0011000']
['0011000']
['1111111']
['1011001']
['0011001']
['0011001']
['0111100']
['0100100']
['0100100']
['0100100']
['1100110']]
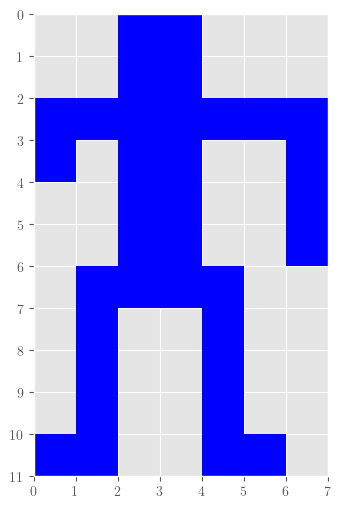
“Pictures have actually been transmitted from Earth into outer space in this way.
Two large prime numbers were used so that a much more detailed picture could be sent.
It is reasonable to expect that a civilized recipient of such a message would be able to work out how to reconstruct the picture, since factorization of a number into prime factors is a property independent of language or notation.”
[1.2]#
Suppose the binary repetition code of length \(5\) is used for a binary symmetric channel which has symbol error probability \(p\).
Show that the word error probability of the code is
\( 10p^3-15p^4+6p^5 \)
See the page on the binary repetition code of length \(5\).
[1.3]#
Show that a code \(C\) having minimum distance \(d(C)=4\) can be used simultaneously to correct single errors and detect double errors.
[\(C\) could also be used either as a single-error-correcting code or as a triple-error-detecting code, but not both simultaneously. Why not?]
\( \begin{aligned} d(C)\ge4&=(s=3)+1 \\ d(C)\ge4&=2(t=1.5)+1 \end{aligned} \)
Suppose the vector \(\mathbf{y}\) is received.
If \(d(\mathbf{x,y})\le1\) for some codeword \(\mathbf{x}\in C\), then \(\mathbf{y}\) is closer to \(\mathbf{x}\) than to any other codeword and so it will be decoded to it (and thus corrected).
If \(d(\mathbf{x,y})\ge2\) for all codewords \(\mathbf{x}\in C\), then \(\mathbf{y}\) is equally distant from them all and so cannot be decoded to a closest codeword; and it is not a codeword; so, it can be detected.
Why is this d(x,y)>=2, and not just d(x,y)=2?
If \(d(\mathbf{x,y})=3\) for some codeword \(\mathbf{x}\in C\), then \(\mathbf{y}\) is not a codeword by the minimum distance \(d(C)=4\) of the code.
But it could be the case that \(d(\mathbf{x',y})\le1\) for some other codeword \(\mathbf{x'\ne x}\in C\).
In an error-correcting context, \(\mathbf{y}\) would be decoded to \(\mathbf{x'}\).
[1.4]#
The code used by Mariner 9 will correct any received \(32\)-tuple provided not more than how many errors have occurred?
See the page on the \((32,64,16)\) Reed-Muller code.
[1.5]#
(i) Show that a \(3\)-ary \((3,M,2)\)-code must have \(M\le9\).
Suppose \(C\) is a \((3,M,2)\)-code.
The \(M\) ordered pairs obtained by deleting the third coordinate of each codeword must be distinct; for if any two were identical, then the corresponding codewords would differ only in the third position contradicting \(d(C)=2\).
Therefore, \(M\le q^2\).
(ii) Show that a \(3\)-ary \((3,9,2)\)-code exists.
(iii) Generalize the results of (i) and (ii) to \(q\)-ary \((3,M,2)\)-codes, for any integer \(q\ge2\).
\( \{(a,b,(a+b)\mod q)\mid(a,b)\in(F_q)^2\} \)
is a \(q\)-ary \((3,q^2,2)\)-code.
q=2,(3,4,2)-code#
\( \begin{aligned} (3,4,2)&\text{-code}\subseteq(F_2)^3 \end{aligned} \)
q=2
n=3
f=fqn(q,n)
M=fqn(q,2)
C=[list(m+str(sum([int(i) for i in m])%q) for m in sorted(list(M)))]
for k in range(q-1):
C.append(list(''.join([str((int(i)+1)%q) for i in m]) for m in C[k]))
print(f"{q**n:,}")
print(f)
print(M)
pd.DataFrame(data=C)
8
{'001', '000', '010', '011', '111', '110', '100', '101'}
{'00', '01', '11', '10'}
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 000 | 011 | 101 | 110 |
| 1 | 111 | 100 | 010 | 001 |
q=3,(3,9,2)-code#
\( \begin{aligned} (3,9,2)&\text{-code}\subseteq(F_3)^3 \end{aligned} \)
q=3
n=3
f=fqn(q,n)
M=fqn(q,2)
C=[list(m+str(sum([int(i) for i in m])%q) for m in sorted(list(M)))]
for k in range(q-1):
C.append(list(''.join([str((int(i)+1)%q) for i in m]) for m in C[k]))
print(f"{q**n:,}")
print(f)
print(M)
pd.DataFrame(data=C)
27
{'200', '211', '021', '112', '020', '221', '212', '010', '000', '002', '122', '222', '220', '001', '102', '022', '012', '121', '202', '110', '210', '201', '120', '011', '111', '100', '101'}
{'02', '00', '11', '22', '01', '12', '21', '20', '10'}
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 000 | 011 | 022 | 101 | 112 | 120 | 202 | 210 | 221 |
| 1 | 111 | 122 | 100 | 212 | 220 | 201 | 010 | 021 | 002 |
| 2 | 222 | 200 | 211 | 020 | 001 | 012 | 121 | 102 | 110 |
q=4,(3,16,2)-code#
\( \begin{aligned} (3,16,2)&\text{-code}\subseteq(F_4)^3 \end{aligned} \)
q=4
n=3
f=fqn(q,n)
M=fqn(q,2)
C=[list(m+str(sum([int(i) for i in m])%q) for m in sorted(list(M)))]
for k in range(q-1):
C.append(list(''.join([str((int(i)+1)%q) for i in m]) for m in C[k]))
print(f"{q**n:,}")
print(f)
print(M)
pd.DataFrame(data=C)
64
{'302', '200', '231', '211', '230', '311', '130', '301', '021', '303', '003', '112', '323', '313', '020', '221', '212', '312', '010', '000', '013', '321', '331', '131', '322', '002', '031', '122', '113', '310', '133', '213', '222', '320', '220', '032', '232', '001', '102', '332', '223', '233', '330', '103', '022', '012', '121', '202', '110', '300', '210', '023', '203', '201', '030', '033', '120', '123', '132', '333', '011', '111', '100', '101'}
{'31', '02', '30', '00', '03', '32', '11', '33', '13', '22', '23', '01', '12', '21', '20', '10'}
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 000 | 011 | 022 | 033 | 101 | 112 | 123 | 130 | 202 | 213 | 220 | 231 | 303 | 310 | 321 | 332 |
| 1 | 111 | 122 | 133 | 100 | 212 | 223 | 230 | 201 | 313 | 320 | 331 | 302 | 010 | 021 | 032 | 003 |
| 2 | 222 | 233 | 200 | 211 | 323 | 330 | 301 | 312 | 020 | 031 | 002 | 013 | 121 | 132 | 103 | 110 |
| 3 | 333 | 300 | 311 | 322 | 030 | 001 | 012 | 023 | 131 | 102 | 113 | 120 | 232 | 203 | 210 | 221 |
q=5,(3,32,2)-code#
\( \begin{aligned} (3,32,2)&\text{-code}\subseteq(F_5)^3 \end{aligned} \)
q=5
n=3
f=fqn(q,n)
M=fqn(q,2)
C=[list(m+str(sum([int(i) for i in m])%q) for m in sorted(list(M)))]
for k in range(q-1):
C.append(list(''.join([str((int(i)+1)%q) for i in m]) for m in C[k]))
print(f"{q**n:,}")
print(f)
print(M)
pd.DataFrame(data=C)
125
{'200', '230', '240', '443', '440', '021', '420', '144', '212', '243', '024', '310', '233', '404', '012', '121', '210', '023', '203', '401', '412', '100', '231', '314', '301', '303', '432', '313', '430', '221', '214', '331', '131', '340', '043', '133', '032', '232', '040', '241', '204', '324', '140', '141', '441', '132', '333', '111', '341', '134', '042', '400', '403', '112', '323', '434', '020', '421', '041', '000', '034', '321', '014', '304', '322', '414', '433', '113', '234', '320', '220', '410', '004', '332', '124', '330', '103', '343', '201', '244', '030', '011', '242', '422', '101', '302', '142', '044', '211', '311', '104', '130', '143', '003', '344', '423', '114', '010', '342', '013', '002', '031', '122', '334', '442', '213', '222', '431', '411', '001', '102', '223', '224', '022', '424', '202', '110', '300', '402', '033', '444', '120', '123', '413', '312'}
{'04', '42', '22', '21', '20', '12', '02', '00', '03', '13', '33', '10', '34', '14', '31', '24', '32', '11', '23', '30', '44', '01', '41', '43', '40'}
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 000 | 011 | 022 | 033 | 044 | 101 | 112 | 123 | 134 | 140 | ... | 303 | 314 | 320 | 331 | 342 | 404 | 410 | 421 | 432 | 443 |
| 1 | 111 | 122 | 133 | 144 | 100 | 212 | 223 | 234 | 240 | 201 | ... | 414 | 420 | 431 | 442 | 403 | 010 | 021 | 032 | 043 | 004 |
| 2 | 222 | 233 | 244 | 200 | 211 | 323 | 334 | 340 | 301 | 312 | ... | 020 | 031 | 042 | 003 | 014 | 121 | 132 | 143 | 104 | 110 |
| 3 | 333 | 344 | 300 | 311 | 322 | 434 | 440 | 401 | 412 | 423 | ... | 131 | 142 | 103 | 114 | 120 | 232 | 243 | 204 | 210 | 221 |
| 4 | 444 | 400 | 411 | 422 | 433 | 040 | 001 | 012 | 023 | 034 | ... | 242 | 203 | 214 | 220 | 231 | 343 | 304 | 310 | 321 | 332 |
5 rows × 25 columns