Assignment 8#
Dave Friedman
CMPSC 465 Algorithms and Data Structures
1#
A cargo plane can carry a maximum weight of \(100\) tons of cargo and a maximum volume of \(60\) cubic meters of cargo in one trip. You are in charge of loading the plane so as to maximize revenue. There are three possible materials that you can ship:
1. Material 1 has a density of \(2\) tons per cubic meter and a revenue of \(\$1,000.00\) per cubic meter shipped. You have \(40\) cubic meters of the material available.
2. Material 2 has a density of \(1\) ton per cubic meter and a revenue of \(\$1,200.00\) per cubic meter shipped. You have \(30\) cubic meters of the material available.
3. Material 3 has a density of \(3\) tons per cubic meter and a revenue of \(\$12,000.00\) per cubic meter shipped. You have \(20\) cubic meters of the material available.
Formulate a linear program that optimizes the amount of revenue within the constraints.
\( \begin{aligned} x_1 &= \text{the number of cubic meters of material } 1 \\ x_2 &= \text{the number of cubic meters of material } 2 \\ x_3 &= \text{the number of cubic meters of material } 3 \\ \end {aligned} \)
\( \max \{ 1000x_1 + 1200x_2 + 12000x_3 \} \text{ s.t.} \\ \begin{aligned} 2x_1 + x_2 + 3x_3 &\le 100 && \text{the total tonnage must be no greater than 100} \\ x_1 + x_2 + x_3 &\le 60 && \text{the total volume must be no greater than 60 cubic meters} \\ x_1 &\le 40 && \text{the total volume of material 1 must be no greater than 40 cubic meters} \\ x_2 &\le 30 && \text{the total volume of material 2 must be no greater than 30 cubic meters} \\ x_3 &\le 20 && \text{the total volume of material 3 must be no greater than 20 cubic meters} \\ x_1, x_2, x_3 &\ge 0 && \text{the total volume of any material must be nonnegative} \\ \end {aligned} \)
2#
Convert the following linear program into standard form, and state whether a solution to the program exists or not.
\( \max \{ 4x_1 + 2x_3 - 8x_3 + x_4 \} \text{ s.t.} \\ \begin{aligned} x_1 + x_2 &\ge 5 \\ x_2 &\le 10 \\ x_1 + x_3 &\le 7 \\ x_2 + x_3 &\ge 3 \\ x_4 &\le 3 \\ x_4 &\ge -5 \\ \end {aligned} \)
\( \min \{ -4x_1 - 2x_3 + 8x_3 - x_4 \} \text{ s.t.} \\ \begin{aligned} x_1 + x_2 - s_1 &= 5 \\ x_2 + s_2 &= 10 \\ x_1 + x_3 + s_3 &= 7 \\ x_2 + x_3 - s_4 &= 3 \\ x_4 + s_5 &= 3 \\ x_4^+ - x_4^- - s_6 &= -5 \\ x_1, x_2, x_3, x_4, x_4^+, x_4^-, s_1, s_2, s_3, s_4, s_5, s_6 &\ge 0 \\ \end {aligned} \)
The solution exists.
3#
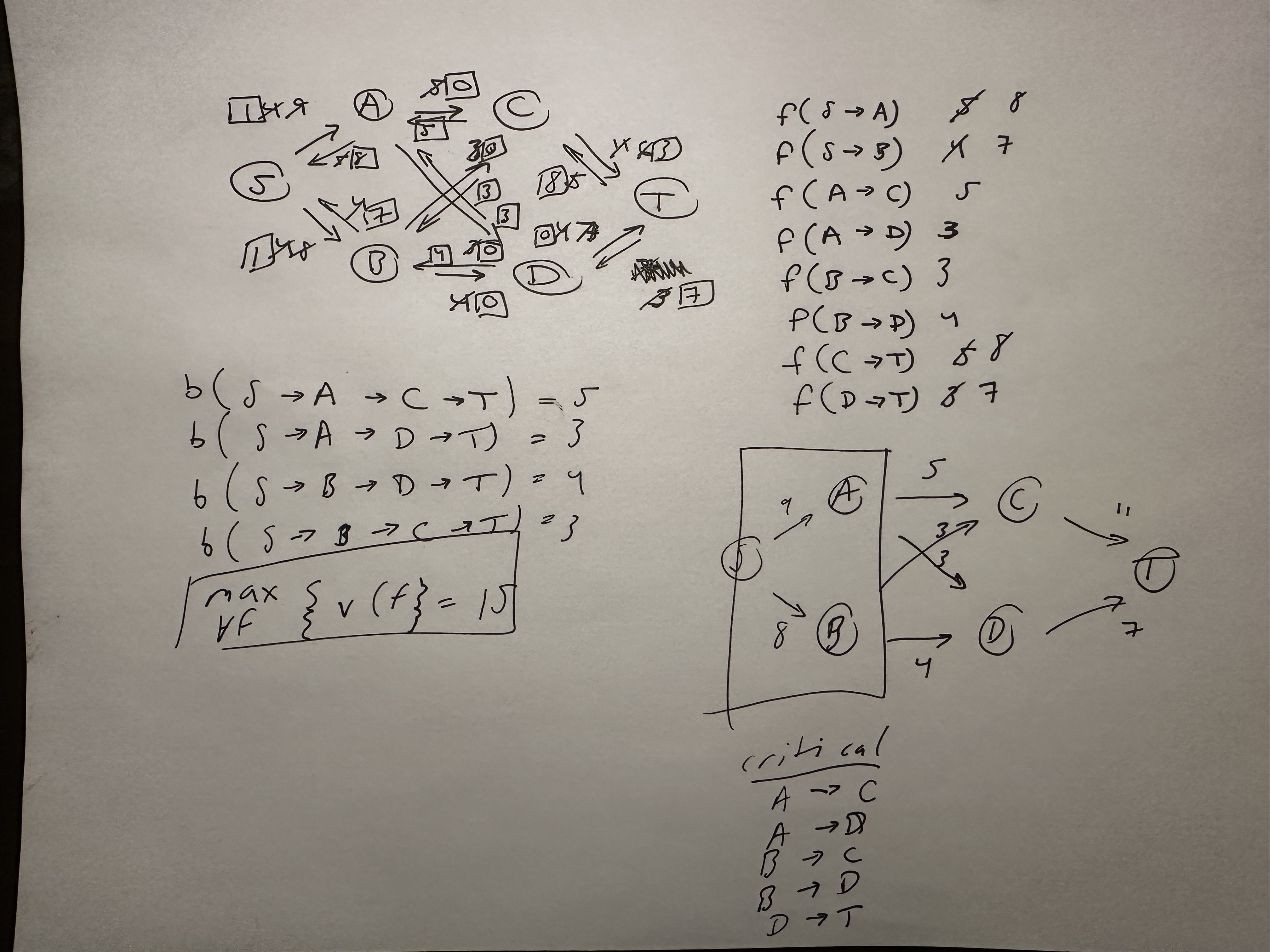
Consider the following flow network with source \(S\) and sink \(T\) and associated edge capacities.
A
Find the maximum flow and all possible minimum cuts.
B
Draw the residual graph \(G_f\) along with its edge capacities where \(f\) is the max flow from part A.
C
List all critical edges within the network.