Double Integration#
Revised
22 Mar 2023
Imports & Environment#
Show code cell source
import numpy as np
import matplotlib as mpl
from matplotlib import cm
import matplotlib.pyplot as plt
from matplotlib.ticker import LinearLocator
#mpl.projections.get_projection_names()
#plt.style.available
from scipy import integrate
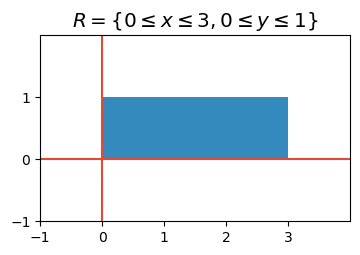
\(\begin{aligned}&\underset{R}{\iint}(1+2xy^3)\,dA\,\,\,\text{where}\,R=\{0\le x\le3,0\le y\le1\}\\\end{aligned}\)#
[8.1A]
\( \boxed{ \begin{aligned} \frac{21}{4} =\underset{R}{\iint}(1+2xy^3)\,dA \,\,\,\text{where}\,R=\{0\le x\le3,0\le y\le1\} \end{aligned} } \)
Show code cell source
x1,x2=0,3
y1,y2=0,1
f = 4
fig = plt.figure(figsize=(f,f));
ax = plt.subplot();
plt.style.use('ggplot');
ax.set_aspect(1);
ax.add_patch(mpl.patches.Rectangle((x1,y1),x2-x1,y2-y1));
ax.set_xticks(np.arange(x1-1,x2+1,1));
ax.set_xlim(x1-1,x2+1);
ax.set_yticks(np.arange(y1-1,y2+1,1));
ax.set_ylim(y1-1,y2+1);
ax.axhline(0);
ax.axvline(0);
ax.set_title('$R=\\{0\\leq x\\leq3,0\\leq y\\leq1\\}$');
\( \boxed{ dA=dx\,dy } \)
\( \begin{aligned} &\underset{R}{\iint}(1+2xy^3)\,dA \,\,\,\text{where}\,R=\{0\le x\le3,0\le y\le1\}\\ &=\int_{y=0}^{y=1}\int_{x=0}^{x=3}(1+2xy^3)\,dx\,dy\\ &=\int_{y=0}^{y=1}(x+x^2y^3)\Big|_{x=0}^{x=3}\,dy\\ &=\int_{y=0}^{y=1}(3+9y^3)\,dy\\ &=\left.\left(3y+\frac{9}{4}y^4\right)\right|_{y=0}^{y=1}\\ &=3+\frac{9}{4}\\ &=\frac{21}{4} \end{aligned} \)
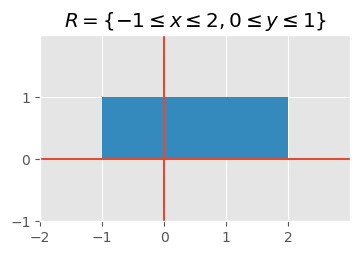
\(\begin{aligned}\underset{R}{\iint}(6x-3y^2+4xy)\,dA\,\,\,\text{where}\,R=\{-1\le x\le2,0\le y\le1\}\\\end{aligned}\)#
[8.1B]
\( \boxed{ \begin{aligned} 9 =\underset{R}{\iint}(6x-3y^2+4xy)\,dA \,\,\,\text{where}\,R=\{-1\le x\le2,0\le y\le1\} \end{aligned} } \)
Show code cell source
x1,x2=-1,2
y1,y2= 0,1
f = 4
fig = plt.figure(figsize=(f,f));
ax = plt.subplot();
plt.style.use('ggplot');
ax.set_aspect(1);
ax.add_patch(mpl.patches.Rectangle((x1,y1),x2-x1,y2-y1));
ax.set_xticks(np.arange(x1-1,x2+1,1));
ax.set_xlim(x1-1,x2+1);
ax.set_yticks(np.arange(y1-1,y2+1,1));
ax.set_ylim(y1-1,y2+1);
ax.axhline(0);
ax.axvline(0);
ax.set_title('$R=\\{-1\\leq x\\leq2,0\\leq y\\leq1\\}$');
\( \boxed{ dA=dx\,dy } \)
\( \begin{aligned} &\underset{R}{\iint}(6x-3y^2+4xy)\,dA \,\,\,\text{where}\,R=\{-1\le x\le2,0\le y\le1\}\\ &=\int_{y=0}^{y=1}\int_{x=-2}^{x=1}(6x-3y^2+4xy)\,dx\,dy\\ &=\int_{y=0}^{y=1}\left.\left(6\left(\frac{1}{2}x^2\right)-3xy^2+4\left(\frac{1}{2}x^2\right)y\right)\right|_{x=-1}^{x=2}\,dy\\ &=\int_{y=0}^{y=1}(3x^2-3xy^2+2x^2y)\Big|_{x=-1}^{x=2}\,dy\\ &=\int_{y=0}^{y=1}[(3(2)^2-3(2)y^2+2(2)^2y)-(3(-1)^2-3(-1)y^2+2(-1)^2y)]\,dy\\ &=\int_{y=0}^{y=1}[(12-6y^2+8y)-(3+3y^2+2y)]\,dy\\ &=\int_{y=0}^{y=1}(12-6y^2+8y-3-3y^2-2y)\,dy\\ &=\int_{y=0}^{y=1}(9-9y^2+6y)\,dy\\ &=\left.\left(9y-9\left(\frac{1}{3}y^3\right)+6\left(\frac{1}{2}y^2\right)\right)\right|_{y=0}^{y=1}\\ &=\left(9y-3y^3+3y^2\right)\Big|_{y=0}^{y=1}\\ &=(9(1)-3(1)^3+3(1)^2)-(9(0)-3(0)^3+3(0)^2)\\ &=9-3+3\\ &=9\\ \end{aligned} \)
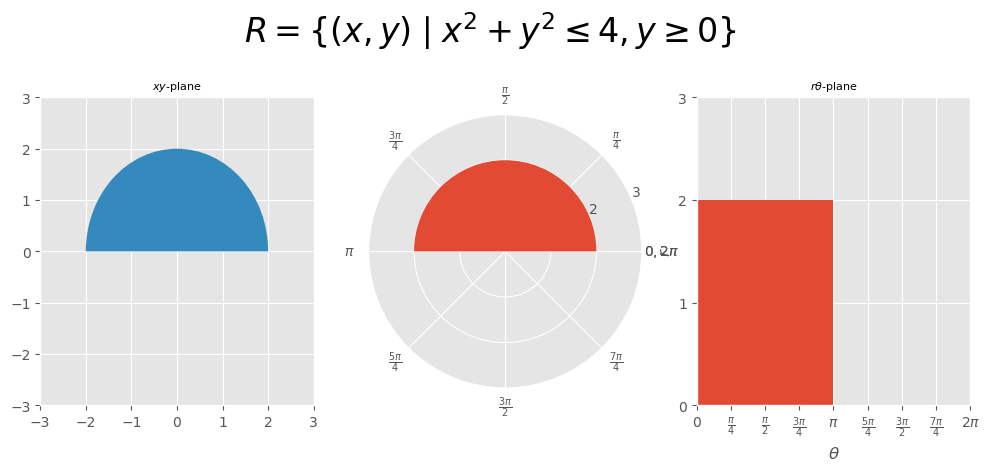
\(\begin{aligned}\underset{R}{\iint}x\sqrt{x^2+y^2}\,dA\,\,\,\text{where}\,R=\{(x,y)\mid x^2+y^2\le4,y\ge0\}\end{aligned}\)#
[03/]
\( \boxed{ \begin{aligned} 0=\underset{R}{\iint}x\sqrt{x^2+y^2}\,dA\,\,\,\text{where}\,R=\{(x,y)\mid x^2+y^2\le4,y\ge0\} \end{aligned} } \)
Show code cell source
r1,r2=0,2
t1,t2=0,np.pi
plt.style.use('ggplot');
fig = plt.figure(figsize=(12,4));
ax1 = plt.subplot(131,projection='rectilinear');
ax1.add_patch(mpl.patches.Wedge((0,0),r=r2,theta1=0,theta2=180));
ax1.set_xticks(ticks=np.arange(-3,4,1));
ax1.set_xlim(-3,3);
ax1.set_yticks(ticks=np.arange(-3,4,1));
ax1.set_ylim(-3,3);
ax1.set_title('$xy$-plane', fontsize=8);
ax2 = plt.subplot(132,projection='polar');
ax2.bar(x=t2-(t2-t1)/2,height=r2-r1,width=t2-t1,bottom=r1);
ax2.set_rticks(ticks =np.arange(0,8,1),
labels=['','1','2','3','4','5','6','7']);
ax2.set_xticks(ticks =np.arange(0,9*np.pi/4,np.pi/4),
labels=[
'$0,2\\pi$',
'$\\frac{\\pi}{4}$',
'$\\frac{\\pi}{2}$',
'$\\frac{3\\pi}{4}$',
'$\\pi$',
'$\\frac{5\\pi}{4}$',
'$\\frac{3\\pi}{2}$',
'$\\frac{7\\pi}{4}$',
'$0,2\\pi$'
]);
ax2.set_rmax(3);
ax2.grid(True);
ax3 = plt.subplot(133, projection='rectilinear');
ax3.bar(x=t2-(t2-t1)/2,height=r2-r1,width=t2-t1,bottom=r1);
ax3.set_xticks(ticks =np.arange(0,9*np.pi/4,np.pi/4),
labels=[
'$0$',
'$\\frac{\\pi}{4}$',
'$\\frac{\\pi}{2}$',
'$\\frac{3\\pi}{4}$',
'$\\pi$',
'$\\frac{5\\pi}{4}$',
'$\\frac{3\\pi}{2}$',
'$\\frac{7\\pi}{4}$',
'$2\\pi$'
]);
ax3.set_xlim(0,2*np.pi);
ax3.set_xlabel('$\\theta$');
ax3.set_yticks(ticks =np.arange(0,8,1));
ax3.set_ylim(0,3);
ax3.set_ylabel('$r$');
ax3.set_title('$r\\theta$-plane', fontsize=8);
ax3.grid(True);
fig.suptitle('$R=\{(x,y)\\mid x^2+y^2\\leq4,y\\geq0\}$', fontsize=24, y=1.1);
\( \boxed{ \begin{aligned} x&=r\cos\theta\\ y&=r\sin\theta\\ x^2+y^2&=r^2\\ dA&=r\,dr\,d\theta\\ \end{aligned} } \)
\( \begin{aligned} x^2+y^2\le4 \implies r^2\le4 \implies \sqrt{r^2}\le\sqrt{4} \implies 0\le r\le2 \end{aligned} \)
\( \begin{aligned} y\ge0 \implies r\sin\theta\ge0 \implies \sin\theta\ge0 \implies 0\le\theta\le\pi \end{aligned} \)
\( \begin{aligned} &\underset{R}{\iint}x\sqrt{x^2+y^2}\,dA\,\,\,\text{where}\,R=\{(x,y)\mid x^2+y^2\le4,y\ge0\}\\ &=\int_{\theta=0}^{\theta=\pi}\int_{r=0}^{r=2} r\cos\theta\sqrt{r^2}\,r\,dr\,d\theta =\int_{\theta=0}^{\theta=\pi}\int_{r=0}^{r=2} r^3\cos\theta\,dr\,d\theta &&\,\,\,\text{by transformation equations}\\ &=\int_{\theta=0}^{\theta=\pi}\cos\theta\,d\theta\int_{r=0}^{r=2} r^3\,dr &&\,\,\,\text{by factoring}\\ &=\left.(\sin\theta)\right|_{\theta=0}^{\theta=\pi} \left.\left(\frac{r^4}{4}\right)\right|_{r=0}^{r=2}\\ &=\cancel{[(\sin(\pi))-(\sin(0))]}\left[\left(\frac{(2)^4}{4}\right)-\left(\frac{(0)^4}{4}\right)\right]\\ &=0\\ \end{aligned} \)
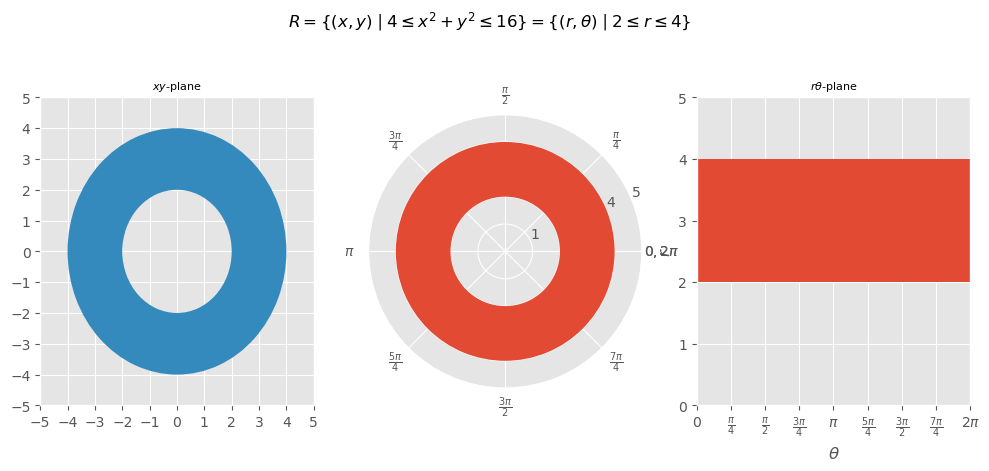
\(\begin{aligned}\underset{R}{\iint}\frac{1}{x^2+y^2}\,dA\,\,\,\text{where}\,R=\{(x,y)\mid 4\le x^2+y^2\le16\}\end{aligned}\)#
[03/]
Calculate the mass of a washer whose inner radius \(r_1\) is
\(r_1=2\,\text{cm}\)
whose outer radius \(r_2\) is
\(r_2=4\,\text{cm}\)
and whose density \(\rho\) is
\( \begin{aligned} \rho(x,y)=\frac{1}{x^2+y^2}\,\text{g cm}^2 \end{aligned} \)
\( \boxed{ \begin{aligned} 2\pi\ln(2) =\underset{R}{\iint}\rho(x,y)\,dA =\underset{R}{\iint}\frac{1}{x^2+y^2}\,dA \,\,\,\text{where}\,R=\{(x,y)\mid 4\le x^2+y^2\le16\} \end{aligned} } \)
Show code cell source
r1,r2=2,4
t1,t2=0,2*np.pi
plt.style.use('ggplot');
fig = plt.figure(figsize=(12,4));
ax1 = plt.subplot(131,projection='rectilinear');
ax1.add_patch(mpl.patches.Wedge((0,0),r=r2,theta1=0,theta2=360,width=r2-r1));
ax1.set_xticks(ticks=np.arange(-(r2+1),r2+2,1));
ax1.set_xlim(-(r2+1),r2+1);
ax1.set_yticks(ticks=np.arange(-(r2+1),r2+2,1));
ax1.set_ylim(-(r2+1),r2+1);
ax1.set_title('$xy$-plane', fontsize=8);
ax2 = plt.subplot(132,projection='polar');
ax2.bar(x=t2-(t2-t1)/2,height=r2-r1,width=t2-t1,bottom=r1);
ax2.set_rticks(ticks =np.arange(0,8,1),
labels=['','1','2','3','4','5','6','7']);
ax2.set_xticks(ticks =np.arange(0,9*np.pi/4,np.pi/4),
labels=[
'$0,2\\pi$',
'$\\frac{\\pi}{4}$',
'$\\frac{\\pi}{2}$',
'$\\frac{3\\pi}{4}$',
'$\\pi$',
'$\\frac{5\\pi}{4}$',
'$\\frac{3\\pi}{2}$',
'$\\frac{7\\pi}{4}$',
'$0,2\\pi$'
]);
ax2.set_rmax(r2+1);
ax2.grid(True);
ax3 = plt.subplot(133, projection='rectilinear');
ax3.bar(x=t2-(t2-t1)/2,height=r2-r1,width=t2-t1,bottom=r1);
ax3.set_xticks(ticks =np.arange(0,9*np.pi/4,np.pi/4),
labels=[
'$0$',
'$\\frac{\\pi}{4}$',
'$\\frac{\\pi}{2}$',
'$\\frac{3\\pi}{4}$',
'$\\pi$',
'$\\frac{5\\pi}{4}$',
'$\\frac{3\\pi}{2}$',
'$\\frac{7\\pi}{4}$',
'$2\\pi$'
]);
ax3.set_xlim(0,2*np.pi);
ax3.set_xlabel('$\\theta$');
ax3.set_yticks(ticks =np.arange(0,8,1));
ax3.set_ylim(0,r2+1);
ax3.set_ylabel('$r$');
ax3.set_title('$r\\theta$-plane', fontsize=8);
ax3.grid(True);
fig.suptitle('$R=\\{(x,y)\\mid 4\\leq x^2+y^2\\leq16\\}=\\{(r,\\theta)\\mid 2\\leq r\\leq4\\}$', fontsize=12, y=1.1);
\( \begin{aligned} &\underset{R}{\iint}\frac{1}{x^2+y^2}\,dA \,\,\,\text{where}\,R=\{(x,y)\mid 4\le x^2+y^2\le16\} \end{aligned} \)
\( \boxed{ \begin{aligned} x&=r\cos\theta\\ y&=r\sin\theta\\ x^2+y^2&=r^2\\ dA&=r\,dr\,d\theta\\ \end{aligned} } \)
\( \begin{aligned} 4\le x^2+y^2\le16 \implies 2^2\le r^2\le4^2 \implies \sqrt{2^2}\le\sqrt{r^2}\le\sqrt{4^2} \implies 2\le r\le4 \end{aligned} \)
\( \begin{aligned} &\underset{R}{\iint}\frac{1}{x^2+y^2}\,dA \,\,\,\text{where}\,R=\{(x,y)\mid 4\le x^2+y^2\le16\} \\ &=\int_{\theta=0}^{\theta=2\pi}\int_{r=2}^{r=4}\frac{1}{r^2}\,r\,dr\,d\theta =\int_{\theta=0}^{\theta=2\pi}\int_{r=2}^{r=4}\frac{1}{r}\,dr\,d\theta &&\,\,\,\text{by transformation equations} \\ &=\int_{\theta=0}^{\theta=2\pi}\,d\theta\int_{r=2}^{r=4}\frac{1}{r}\,dr &&\,\,\,\text{by factoring} \\ &=\left.(\theta)\right|_{\theta=0}^{\theta=2\pi} \left.\ln(|r|)\right|_{r=2}^{r=4} =\left.(\theta)\right|_{\theta=0}^{\theta=2\pi} \left.\ln(r)\right|_{r=2}^{r=4} &&\,\,\,|r|=r\,\text{by the bounds of}\,r \\ &=2\pi(\ln(4)-\ln(2))\\ &=2\pi\ln(2) \end{aligned} \)
\(\begin{aligned}\underset{R}{\iint}x^2\,dA\,\,\,\text{where R is the part of the unit disk in the second quadrant}\end{aligned}\)#
[R 03/16]
\( \boxed{ \begin{aligned} \frac{\pi}{16} =\underset{R}{\iint}x^2\,dA \,\,\,\text{where R is the part of the unit disk in the second quadrant} \end{aligned} } \)
Show code cell source
r1,r2=0,1
t1,t2=np.pi/2,np.pi
plt.style.use('ggplot');
fig = plt.figure(figsize=(12,4));
ax1 = plt.subplot(131,projection='rectilinear');
ax1.add_patch(mpl.patches.Wedge((0,0),r=1,theta1=90,theta2=180));
ax1.set_xticks(ticks=np.arange(-2,3,1));
ax1.set_xlim(-2,2);
ax1.set_yticks(ticks=np.arange(-2,3,1));
ax1.set_ylim(-2,2);
ax1.set_title('$xy$-plane', fontsize=8);
ax2 = plt.subplot(132,projection='polar');
ax2.bar(x=t2-(t2-t1)/2,height=r2-r1,width=t2-t1,bottom=r1);
ax2.set_rticks(ticks =np.arange(0,8,1),
labels=['','1','2','3','4','5','6','7']);
ax2.set_xticks(ticks =np.arange(0,9*np.pi/4,np.pi/4),
labels=[
'$0,2\\pi$',
'$\\frac{\\pi}{4}$',
'$\\frac{\\pi}{2}$',
'$\\frac{3\\pi}{4}$',
'$\\pi$',
'$\\frac{5\\pi}{4}$',
'$\\frac{3\\pi}{2}$',
'$\\frac{7\\pi}{4}$',
'$0,2\\pi$'
]);
ax2.set_rmax(2);
ax2.grid(True);
ax3 = plt.subplot(133, projection='rectilinear');
ax3.bar(x=t2-(t2-t1)/2,height=r2-r1,width=t2-t1,bottom=r1);
ax3.set_xticks(ticks =np.arange(0,9*np.pi/4,np.pi/4),
labels=[
'$0$',
'$\\frac{\\pi}{4}$',
'$\\frac{\\pi}{2}$',
'$\\frac{3\\pi}{4}$',
'$\\pi$',
'$\\frac{5\\pi}{4}$',
'$\\frac{3\\pi}{2}$',
'$\\frac{7\\pi}{4}$',
'$2\\pi$'
]);
ax3.set_xlim(0,2*np.pi);
ax3.set_xlabel('$\\theta$');
ax3.set_yticks(ticks =np.arange(0,8,1));
ax3.set_ylim(0,2);
ax3.set_ylabel('$r$');
ax3.set_title('$r\\theta$-plane', fontsize=8);
ax3.grid(True);
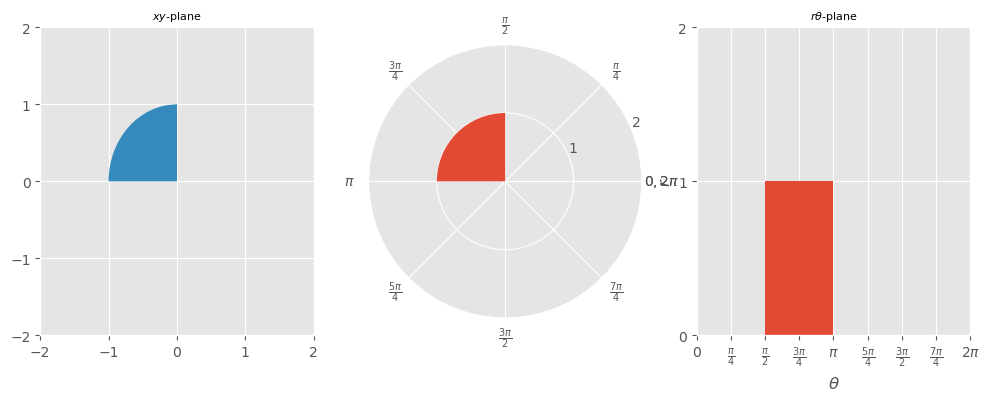
\( \boxed{ \begin{aligned} x&=r\cos\theta\\ y&=r\sin\theta\\ x^2+y^2&=r^2\\ dA&=r\,dr\,d\theta\\ \end{aligned} } \)
\( \begin{aligned} &\underset{R}{\iint}x^2\,dA \,\,\,\text{where R is the part of the unit disk in the second quadrant}\\ &=\int_{\theta=\frac{\pi}{2}}^{\theta=\pi}\int_{r=0}^{r=1} (r\cos\theta)^2\,r\,dr\,d\theta =\int_{\theta=\frac{\pi}{2}}^{\theta=\pi}\int_{r=0}^{r=1} r^3\cos^2\theta\,dr\,d\theta &&\,\,\,\text{by transformation equations}\\ &=\int_{\theta=\frac{\pi}{2}}^{\theta=\pi}\cos^2\theta\,d\theta\int_{r=0}^{r=1} r^3\,dr &&\,\,\,\text{by factoring}\\ &=\int_{\theta=\frac{\pi}{2}}^{\theta=\pi}\left(\frac{1+\cos(2\theta)}{2}\right)\,d\theta\int_{r=0}^{r=1} r^3\,dr =\frac{1}{2}\int_{\theta=\frac{\pi}{2}}^{\theta=\pi}1+\cos(2\theta)\,d\theta\int_{r=0}^{r=1} r^3\,dr &&\,\,\,\text{by the half-angle identity}\\ &=\frac{1}{2}\left.\left(\theta+\frac{\sin(2\theta)}{2}\right)\right|_{\theta=\frac{\pi}{2}}^{\theta=\pi}\left.\left(\frac{r^4}{4}\right)\right|_{r=0}^{r=1}\\ &=\frac{1}{2}\left(\left((\pi)+\frac{\sin(2(\pi))}{2}\right)-\left(\left(\frac{\pi}{2}\right)+\frac{\sin\left(2\left(\frac{\pi}{2}\right)\right)}{2}\right)\right)\left(\left(\frac{(1)^4}{4}\right)-\cancel{\left(\frac{(0)^4}{4}\right)}\right)\\ &=\frac{1}{2}\left(\left(\pi+\cancel{\frac{\sin(2\pi)}{2}}\right)-\left(\frac{\pi}{2}+\cancel{\frac{\sin\pi}{2}}\right)\right)\left(\frac{1}{4}\right)\\ &=\frac{1}{8}\left(\pi-\frac{\pi}{2}\right)=\frac{1}{8}\left(\frac{\pi}{2}\right)\\ &=\frac{\pi}{16}\\ \end{aligned} \)
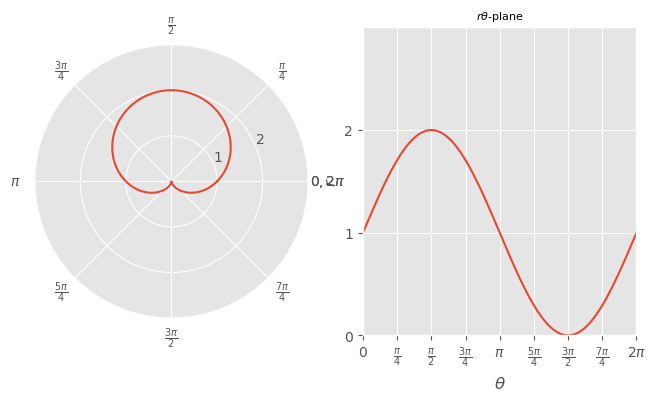
Cartioid#
[R 03/16]
\( r=1+\sin\theta \) defines a cartioid
\( \begin{aligned} \theta&=0&&\implies r=1\\ \theta&=\frac{\pi}{2}&&\implies r=2\\ \theta&=\pi&&\implies r=1\\ \theta&=\frac{3\pi}{2}&&\implies r=0\\ \end{aligned} \)
Show code cell source
t =np.arange((0/4)*np.pi, (8/4)*np.pi, 0.01)
r2=1+np.sin(t)
plt.style.use('ggplot');
fig = plt.figure(figsize=(12,4));
ax2 = plt.subplot(132,projection='polar');
ax2.plot(t,r2);
ax2.set_rticks(ticks =np.arange(0,8,1),
labels=['','1','2','3','4','5','6','7']);
ax2.set_xticks(ticks =np.arange(0,9*np.pi/4,np.pi/4),
labels=[
'$0,2\\pi$',
'$\\frac{\\pi}{4}$',
'$\\frac{\\pi}{2}$',
'$\\frac{3\\pi}{4}$',
'$\\pi$',
'$\\frac{5\\pi}{4}$',
'$\\frac{3\\pi}{2}$',
'$\\frac{7\\pi}{4}$',
'$0,2\\pi$'
]);
ax2.set_rmax(np.max(r2)+1);
ax2.grid(True);
ax3 = plt.subplot(133, projection='rectilinear');
ax3.plot(t,r2);
ax3.set_xticks(ticks =np.arange(0,9*np.pi/4,np.pi/4),
labels=[
'$0$',
'$\\frac{\\pi}{4}$',
'$\\frac{\\pi}{2}$',
'$\\frac{3\\pi}{4}$',
'$\\pi$',
'$\\frac{5\\pi}{4}$',
'$\\frac{3\\pi}{2}$',
'$\\frac{7\\pi}{4}$',
'$2\\pi$'
]);
ax3.set_xlim(0,2*np.pi);
ax3.set_xlabel('$\\theta$');
ax3.set_yticks(ticks =np.arange(0,8,1));
ax3.set_ylim(0,np.max(r2)+1);
ax3.set_ylabel('$r$');
ax3.set_title('$r\\theta$-plane', fontsize=8);
ax3.grid(True);
fig.suptitle('', fontsize=12, y=1.1);
A microphone’s pickup is the region surrounding the microphone from which the microphone gathers sound.
circular pickup
captures too much of the audience
straight-directional pickup
captures no audience
cartioid (heart-shaped) pickup
captures the first few rows of the audience
What percentage of the cartioid is on stage, or band-capturing, as opposed to off stage, or audience-capturing?
\( \begin{aligned} ?\,\%=\frac{A_{\text{on stage}}}{A_{\text{total}}}\times100 \end{aligned} \)
\( \boxed{ \begin{aligned} x&=r\cos\theta\\ y&=r\sin\theta\\ x^2+y^2&=r^2\\ dA&=r\,dr\,d\theta\\ \end{aligned} } \)
\( \begin{aligned} &A =\underset{R}{\iint}\,dA \,\,\,\text{where}\,R=\{\theta_1\le\theta\le\theta_2,0\le r\le1+\sin\theta\} \end{aligned} \)
\( \begin{aligned} &=\int_{\theta_1}^{\theta_2}\int_{r=0}^{r=1+\sin\theta}\,r\,dr\,d\theta &&\,\,\,\text{by transformation equations} \\ &=\int_{\theta_1}^{\theta_2}\left.\left(\frac{r^2}{2}\right)\right|_{r=0}^{r=1+\sin\theta}\,d\theta =\frac{1}{2}\int_{\theta_1}^{\theta_2}\left.r^2\right|_{r=0}^{r=1+\sin\theta}\,d\theta \\ &=\frac{1}{2}\int_{\theta_1}^{\theta_2}[(1+\sin\theta)^2-\cancel{(0)^2}]\,d\theta =\frac{1}{2}\int_{\theta_1}^{\theta_2}(1+2\sin\theta+\sin^2\theta)\,d\theta \\ &=\frac{1}{2}\int_{\theta_1}^{\theta_2}\left(1+2\sin\theta+\frac{1-\cos(2\theta)}{2}\right)\,d\theta =\frac{1}{2}\int_{\theta_1}^{\theta_2}\left(\frac{3}{2}+2\sin\theta-\frac{\cos(2\theta)}{2}\right)\,d\theta &&\,\,\,\text{by the half-angle identity} \\ &=\frac{1}{2}\left.\left(\frac{3}{2}\theta-2\cos\theta-\frac{\sin(2\theta)}{4}\right)\right|_{\theta_1}^{\theta_2} \end{aligned} \)
\( \begin{aligned} &A_{\text{on stage}} =\underset{R}{\iint}\,dA \,\,\,\text{where}\,R=\{0\le\theta\le\pi,0\le r\le1+\sin\theta\} \\ &=\frac{1}{2}\left.\left(\frac{3}{2}\theta-2\cos\theta-\frac{\sin(2\theta)}{4}\right)\right|_{\theta=0}^{\theta=\pi} \\ &=\frac{1}{2}\left[\left(\frac{3}{2}(\pi)-2\cos(\pi)-\cancel{\frac{\sin(2(\pi))}{4}}\right)-\left(\cancel{\frac{3}{2}(0)}-2\cos(0)-\cancel{\frac{\sin(2(0))}{4}}\right)\right] \\ &=\frac{1}{2}\left(\frac{3}{2}\pi-2\cos(\pi)+2\cos(0)\right) =\frac{3}{4}\pi-\cos(\pi)+\cos(0) =\frac{3}{4}\pi+1+1 \\ &=\frac{3}{4}\pi+2 \end{aligned} \)
\( \begin{aligned} &A_{\text{total}} =\underset{R}{\iint}\,dA \,\,\,\text{where}\,R=\{0\le\theta\le2\pi,0\le r\le1+\sin\theta\} \\ &=\frac{1}{2}\left.\left(\frac{3}{2}\theta-2\cos\theta-\frac{\sin(2\theta)}{4}\right)\right|_{\theta=0}^{\theta=2\pi} \\ &=\frac{1}{2}\left[\left(\frac{3}{2}(2\pi)-2\cos(2\pi)-\cancel{\frac{\sin(2(2\pi))}{4}}\right)-\left(\cancel{\frac{3}{2}(0)}-2\cos(0)-\cancel{\frac{\sin(2(0))}{4}}\right)\right] \\ &=\frac{1}{2}\left(3\pi-2\cos(2\pi)+2\cos(0)\right) =\frac{3}{2}\pi-\cos(2\pi)+\cos(0) =\frac{3}{2}\pi-1+1 \\ &=\frac{3}{2}\pi \end{aligned} \)
\( \begin{aligned} \frac{A_{\text{on stage}}}{A_{\text{total}}}\times100 =\frac{\frac{3}{4}\pi+2}{\frac{3}{2}\pi}\times100 \approx92.4\% \end{aligned} \)
((3/4)*np.pi+2)/((3/2)*np.pi)
0.9244131815783876