Elementary Complex Analysis#
Revised
07 May 2023
Show code cell source
import numpy as np
import matplotlib as mpl
from matplotlib import cm
from matplotlib.ticker import LinearLocator
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
plt.style.use('ggplot');
#mpl.projections.get_projection_names()
#plt.style.available
import scipy
from scipy import integrate
import math
import cmath
from IPython.display import display, Math
from datetime import datetime as d
import locale as l
import platform as p
import sys as s
pad = 20
print(f"{'Executed'.upper():<{pad}}: {d.now()}")
print()
print(f"{'Platform' :<{pad}}: "
f"{p.mac_ver()[0]} | "
f"{p.system()} | "
f"{p.release()} | "
f"{p.machine()}")
print(f"{'' :<{pad}}: {l.getpreferredencoding()}")
print()
print(f"{'Python' :<{pad}}: {s.version}")
print(f"{'' :<{pad}}: {s.version_info}")
print(f"{'' :<{pad}}: {p.python_implementation()}")
print()
print(f"{'Matplotlib' :<{pad}}: {mpl.__version__}")
print(f"{'NumPy' :<{pad}}: {np .__version__}")
print(f"{'SciPy' :<{pad}}: {scipy.__version__}")
EXECUTED : 2025-01-23 15:23:50.001508
Platform : 15.2 | Darwin | 24.2.0 | arm64
: UTF-8
Python : 3.11.11 | packaged by conda-forge | (main, Dec 5 2024, 14:21:42) [Clang 18.1.8 ]
: sys.version_info(major=3, minor=11, micro=11, releaselevel='final', serial=0)
: CPython
Matplotlib : 3.9.3
NumPy : 2.0.2
SciPy : 1.14.1
def translate (z,z0=1+2j):
return z0+z
def scale (z,r=0.5):
return r*z
def rotate90 (z):
"Multiply z by i to rotate by 90 degrees."
return complex(-z.imag,z.real)
def rotate180 (z):
"Multiply z by -1=i^2 to rotate by 180 degrees."
return -z
def rotate270 (z):
"Multiply z by -i=i^3 to rotate by 270 degrees."
return complex(z.imag,-z.real)
def rotate (z,tau):
"Rotate z by tau radians."
return z*cmath.e**(tau*1j)
def uC (z):
"Project a complex number onto the unit circle."
return cmath.e**(1j*cmath.polar(z)[1])
def pC (S,xl=-10,yl=10,dpi=100,t='n',v='n'):
"Plot a set of complex numbers in the complex plane."
fig = plt.figure(dpi=dpi);
ax = plt.subplot();
ax.set_aspect(1);
for s in S:
for x,y in [np.array([[c.real,c.imag] for c in s]).T]:
ax.scatter(x,y);
if v=='y':
ax.quiver([0]*len(x),[0]*len(y),x,y,scale_units='xy',scale=1,width=0.001);
ax.add_patch(plt.Circle((0,0),1,facecolor='None',edgecolor='b'));
ax.set_xticks(ticks=np.arange(xl,yl+1),labels=np.arange(xl,yl+1));
ax.set_yticks(ticks=np.arange(xl,yl+1),labels=[f'{str(c)}i' for c in np.arange(xl,yl+1)]);
ax.set_xlim(xl,yl);
ax.set_ylim(xl,yl);
ax.set_xlabel('Re');
ax.set_ylabel('Im');
What is \(i\)?#
\( \boxed{ i\overset{\text{def}}=\sqrt{-1} } \)
\( \begin{aligned} i^0&=1\\ i^1&=\sqrt{-1}\\ i^2&=(\sqrt{-1})^2=-1\\ i^3&=ii^2=(i)(-1)=-i\\ i^4&=i^2i^2=(-1)(-1)=1=i^0\\ i^5&=ii^4=(i)(1)=i=i^1\\ i^6&=i^2i^4=(-1)(1)=-1=i^2\\ i^7&=ii^2i^4=(i)(-1)(1)=-i=i^3\\ i^8&=i^4i^4=(1)(1)=1=i^0\\ &...\\ i^{4n}&=1\\ i^{4n+1}&=i\\ i^{4n+2}&=-1\\ i^{4n+3}&=-i\\ \end{aligned} \)
where \(n={0,1,2,3,...}\)
def powers_of_i (ns):
for n in range(ns):
yield f"i^{n:>02} = {1j ** n}"
i = powers_of_i(25)
list(i)
['i^00 = (1+0j)',
'i^01 = 1j',
'i^02 = (-1+0j)',
'i^03 = (-0-1j)',
'i^04 = (1+0j)',
'i^05 = 1j',
'i^06 = (-1+0j)',
'i^07 = (-0-1j)',
'i^08 = (1+0j)',
'i^09 = 1j',
'i^10 = (-1+0j)',
'i^11 = (-0-1j)',
'i^12 = (1+0j)',
'i^13 = 1j',
'i^14 = (-1+0j)',
'i^15 = (-0-1j)',
'i^16 = (1+0j)',
'i^17 = 1j',
'i^18 = (-1+0j)',
'i^19 = (-0-1j)',
'i^20 = (1+0j)',
'i^21 = 1j',
'i^22 = (-1+0j)',
'i^23 = (-0-1j)',
'i^24 = (1+0j)']
Complex Numbers#
A complex number is an ordered pair \((a,b)\) where \(a,b\in\mathbb{R}\).
A complex number may take the form
\(z=a+bi\)
z = 3 + 2j
z
(3+2j)
type(z)
complex
The real part of a complex number#
Let \(z=a+bi\) where \(a,b\in\mathbb{R}\) be a complex number.
The real part of \(z\) is
\(\text{Re}(z)=a=a+0i\) where \(a,0\in\mathbb{R}\)
z.real
3.0
The imaginary part of a complex number#
Let \(z=a+bi\) where \(a,b\in\mathbb{R}\) be a complex number.
The imaginary part of \(z\) is
\(\text{Im}(z)=bi=0+bi\) where \(b,0\in\mathbb{R}\)
z.imag * 1j
2j
\( z=\text{Re}(z)+\text{Im}(z) \)
The set of complex numbers \(\mathbb{C}\)#
The set of complex numbers
\( \begin{aligned} \mathbb{C}=\{a+bi\mid a,b\in\mathbb{R}\} \end{aligned} \)
x is imaginary
\( \begin{aligned} x^2&=-1 \implies x=i \\ x^2&=-9 \implies x=3i \\ x^2&=-b \implies x=i\sqrt{b} \end{aligned} \)
x is complex
\( \begin{aligned} (x-1)^2&=-9 \implies x-1=3i \implies x=3i+1 \end{aligned} \)
Properties of complex numbers#
Additive Commutativity#
\( \alpha+\beta=\beta+\alpha \,\,\,\forall\alpha,\beta\in\mathbb{C} \)
PROOF
\(\blacksquare\)
a = (3 + 2j)
b = (5 + 4j)
print(a + b)
print( b + a)
print(a + b == b + a)
(8+6j)
(8+6j)
True
Multiplicative Commutativity#
\( \alpha\beta=\beta\alpha \,\,\,\forall\alpha,\beta\in\mathbb{C} \)
PROOF
Let \(\alpha = a + bi\) and \(\beta = c + di\) where \(a, b, c, d \in \mathbb{R}\).
\( \begin{aligned} \alpha\beta &= (a + bi)(c + di) \\ &= ac + adi + bci + bdi^2 \\ &= (c + di)a + (c + di)bi \\ &= (c + di)(a + bi) \\ &= \beta\alpha \\ \end{aligned} \)
\(\blacksquare\)
a = (3 + 2j)
b = (5 + 4j)
print(a * b)
print( b * a)
print(a * b == b * a)
(7+22j)
(7+22j)
True
Additive Associativity#
\( (\alpha+\beta)+\lambda=\alpha+(\beta+\lambda) \,\,\,\forall\alpha,\beta,\lambda\in\mathbb{C} \)
PROOF
\(\blacksquare\)
a = (3 + 2j)
b = (5 + 4j)
l = (7 + 6j)
print( a + b )
print( b + l )
print((a + b) + l )
print( a + (b + l))
print((a + b) + l == a + (b + l))
(8+6j)
(12+10j)
(15+12j)
(15+12j)
True
Multiplicative Associativity#
\( (\alpha\beta)\lambda=\alpha(\beta\lambda) \,\,\,\forall\alpha,\beta,\lambda\in\mathbb{C} \)
PROOF
\(\blacksquare\)
a = (3 + 2j)
b = (5 + 4j)
l = (7 + 6j)
print( a * b )
print( b * l )
print((a * b) * l )
print( a * (b * l))
print((a * b) * l == a * (b * l))
(7+22j)
(11+58j)
(-83+196j)
(-83+196j)
True
Existence of the additive identity element#
\( \lambda+0=\lambda \,\,\,\forall\lambda\in\mathbb{C},0\in\mathbb{R} \)
PROOF
\(\blacksquare\)
l = 3 + 2j
i = 0 + 0j
print(l )
print( l + i)
print(l == l + i)
(3+2j)
(3+2j)
True
Existence of the multiplicative identity element#
\( \lambda1=\lambda \,\,\,\forall\lambda\in\mathbb{C},1\in\mathbb{R} \)
PROOF
\(\blacksquare\)
l = 3 + 2j
i = 1 + 0j
print(l )
print( l * i)
print(l == l * i)
(3+2j)
(3+2j)
True
Existence of additive inverse elements#
\(\forall \alpha \in \mathbb{C}\), \(\exists \beta \in \mathbb{C}\) s.t. \(\alpha + \beta = 0\)
The additive inverse of an element \(\alpha\) is denoted \(-\alpha\).
PROOF
\(\blacksquare\)
Existence of multiplicative inverse elements#
\(\forall \alpha \in \mathbb{C}\) with \(\alpha \neq 0\), \(\exists \beta \in \mathbb{C}\) s.t. \(\alpha\beta = 1\)
The multiplicative inverse of an element \(\alpha \neq 0\) is denoted \(\alpha^{-1}\).
PROOF
\(\blacksquare\)
Distributivity#
\(\lambda(\alpha + \beta) = \lambda\alpha + \lambda\beta\)
\(\forall \lambda, \alpha, \beta \in \mathbb{C}\)
PROOF
\(\blacksquare\)
Operations on complex numbers#
Complex Addition#
\( (a+bi)+(c+di)=(a+c)+(b+d)i\,\,\,\text{where}\,a,b,c,d\in\mathbb{R} \)
PROOF
\( \begin{aligned} &(a+bi)+(c+di)\\ &=a+bi+c+di\\ &=a+c+bi+di\\ &=(a+c)+(bi+di)\\ &=(a+c)+(b+d)i\\ \end{aligned} \)
\(\blacksquare\)
a=1
b=2
c=3
d=4
display(
complex(a,b) + complex(c,d),
complex((a+c), (b+d)),
complex(a,b) + complex(c,d) == complex((a+c), (b+d)),
)
(4+6j)
(4+6j)
True
Complex Multiplication#
\( (a+bi)(c+di)=(ac-bd)+(ad+bc)i\,\,\,\text{where}\,a,b,c,d\in\mathbb{R} \)
PROOF
\( \begin{aligned} &(a+bi)(c+di)\\ &=ac+adi+bci+bdi^2\\ &=ac+bdi^2+adi+bci\\ &=ac-bd+adi+bci\\ &=(ac-bd)+(adi+bci)\\ &=(ac-bd)+(ad+bc)i\\ \end{aligned} \)
\(\blacksquare\)
a=1
b=2j
c=3
d=4j
display(
(a+b) * (c+d),
complex((a*c - b.imag*d.imag),(a*d.imag + b.imag*c)),
(a+b) * (c+d) == complex((a*c - b.imag*d.imag),(a*d.imag + b.imag*c)),
)
(-5+10j)
(-5+10j)
True
Complex Subtraction#
\( \beta-\alpha\equiv\beta+(-\alpha) \)
a=1
b=2
c=3
d=4
display(
complex(a,b) - complex(c,d),
complex(a,b) + -complex(c,d),
complex(a,b) - complex(c,d) == complex(a,b) + -complex(c,d),
)
(-2-2j)
(-2-2j)
True
Complex Division#
\( \begin{aligned} \frac{\beta}{\alpha}\equiv\beta\alpha^{-1} \end{aligned} \)
Complex arithmetic obeys the same predence rules as real arithmetic.
1+2j*3
(1+6j)
(1+2j)*3
(3+6j)
4*3j**2
(-36+0j)
(4*3j)**2
(-144+0j)
Complex Conjugate of a complex number#
DEFINITION
Let \(z \in \mathbb{C}\).
The complex conjugate of \(z\) is \(\bar{z} \overset{\text{def}}= \,(\text{Re}\, z) - \,(\text{Im}\, z) i\).
If \(z = a + bi\), then \(\bar{z} = a - bi\).
(1+2j).conjugate()
(1-2j)
Absolute Value of a complex number#
DEFINITION
Let \(z \in \mathbb{C}\).
The absolute value of \(z\) is \(|z| \overset{\text{def}}= \sqrt{\,(\text{Re}\, z)^2 + \,(\text{Im}\, z)^2}\).
If \(z = a + bi\), then \(|z| = \sqrt{a^2 + b^2}\).
Claim
\(\forall z \in \mathbb{C}, |z| \ge 0\). (The absolute value of any complex number is nonnegative.)
Proof
This follows from the fact that the sum of squares of a collection of real numbers is nonnegative.
\(\blacksquare\)
Claim
If \(z \in \mathbb{R}\), then \(z = \bar{z}\). (The complex conjugate of a real number is itself.)
Proof
\(z = a + 0i = a = a - 0i = \bar{z}\)
\(\blacksquare\)
abs(1+2j) == np.sqrt(1**2 + 2**2)
np.True_
Operations on a complex number and its conjugate#
Sum of \(z\) and \(\bar{z}\)#
Let \(z \in \mathbb{C}\).
\(z + \bar{z} = 2a\)
Proof
\( \begin{aligned} z + \bar{z} &= (a + bi) + (a - bi) \\ &= a + bi + a - bi \\ &= 2a + bi - bi \\ &= 2a \end{aligned} \)
\(\blacksquare\)
Difference of \(z\) and \(\bar{z}\)#
Let \(z \in \mathbb{C}\).
\(z - \bar{z} = 2bi\)
Proof
\(
\begin{aligned}
z - \bar{z}
&= (a + bi) - (a - bi) \\
&= a + bi - a + bi \\
&= 2bi + a - a \\
&= 2bi
\end{aligned}
\)
\(\blacksquare\)
Product of \(z\) and \(\bar{z}\)#
Let \(z \in \mathbb{C}\).
\(z \bar{z} = |z|^2\)
Proof
\(
\begin{aligned}
z \bar{z}
&= (a + bi) (a - bi) \\
&= a^2 - abi + abi - (bi)^2 \\
&= a^2 - b^2 i^2 \\
&= a^2 + b^2 \\
&= (\sqrt{a^2 + b^2})^2 \\
&= |z|^2
\end{aligned}
\)
\(\blacksquare\)
Properties of the complex conjugate and the absolute value of a complex number#
Additivity of the complex conjugate#
Let \(w, z \in \mathbb{C}\).
\(\overline{w + z} = \bar{w} + \bar{z}\)
Proof
\(
\begin{aligned}
w + z
&= (a + bi) + (c + di) \\
&= (a + c) + (b + d)i \\
\overline{w + z}
&= (a + c) - (b + d)i \\
&= a + c - bi - di \\
&= (a - bi) + (c - di) \\
&= \bar{w} + \bar{z} \\
\end{aligned}
\)
\(\blacksquare\)
Multiplicativity of the complex conjugate#
Let \(w, z \in \mathbb{C}\).
\(\overline{w z} = \bar{w} \bar{z}\)
Proof
\(
\begin{aligned}
w z
&= (a + bi) (c + di) \\
&= ac + adi + bci + bdi^2 \\
&= (ac - bd) + (ad + bc)i \\
\overline{w z}
&= (ac - bd) - (ad + bc)i \\
&= ac - bd - adi - bci \\
&= ac - adi - bci + bdi^2 \\
&= (a - bi) (c - di) \\
&= \bar{w} \bar{z} \\
\end{aligned}
\)
\(\blacksquare\)
Conjugate of the conjugate#
Let \(z \in \mathbb{C}\).
\(\bar{\bar{z}} = z\)
Proof
\(
\begin{aligned}
\bar{z}
&= a - bi \\
&= (a) + (-b)i \\
\bar{\bar{z}}
&= (a) - (-b)i \\
&= a + bi \\
&= z \\
\end{aligned}
\)
\(\blacksquare\)
Boundedness#
Let \(z \in \mathbb{C}\).
\(|a| \le |z|\) and \(|b| \le |z|\)
Proof
\(
\begin{aligned}
|a|
&= \sqrt{a^2} \\
&\le \sqrt{a^2 + b^2} \\
&= |z|
\end{aligned}
\)
\(\blacksquare\)
Absolute value of the complex conjugate#
Let \(z \in \mathbb{C}\).
\(|\bar{z}| = |z|\)
Proof
\(
\begin{aligned}
\bar{z}
&= a - bi \\
&= (a) + (-b)i \\
|\bar{z}|
&= \sqrt{(a)^2 + (-b)^2} \\
&= \sqrt{a^2 + b^2} \\
&= |z| \\
\end{aligned}
\)
\(\blacksquare\)
Multiplicativity of the absolute value#
Let \(w, z \in \mathbb{C}\).
\(|w||z| = |wz|\)
Proof
\(
\begin{aligned}
wz
&= (a + bi) (c + di) \\
&= ac + adi + bci + bdi^2 \\
&= (ac - bd) + (ad + bc)i \\
|wz|
&= \sqrt{(ac - bd)^2 + (ad + bc)^2} \\
&= \sqrt{(ac)^2 - 2abcd + (bd)^2 + (ad)^2 + 2abcd + (bc)^2} \\
&= \sqrt{(ac)^2 + (bd)^2 + (ad)^2 + (bc)^2} \\
&= \sqrt{(ac)^2 + (ad)^2 + (bd)^2 + (bc)^2} \\
&= \sqrt{a^2(c^2 + d^2) + b^2(c^2 + d^2)} \\
&= \sqrt{(a^2 + b^2)(c^2 + d^2)} \\
&= \sqrt{a^2 + b^2} \sqrt{c^2 + d^2} \\
&= |w||z| \\
\end{aligned}
\)
\(\blacksquare\)
Triangle Inequality#
Let \(w, z \in \mathbb{C}\).
\(|w + z| \le |w| + |z|\)
Proof
\(
\begin{aligned}
|w + z|^2
&= (w + z)(\bar{w} + \bar{z}) \\
&= w \bar{w} + z \bar{z} + w \bar{z} + z \bar{w} \\
&= |w|^2 + |z|^2 + w \bar{z} + \overline{w \bar{z}} \\
&= |w|^2 + |z|^2 + w \bar{z} + 2 \,\text{Re}\, (w \bar{z}) \\
&\le |w|^2 + |z|^2 + w \bar{z} + 2 |w \bar{z}| \\
&= |w|^2 + |z|^2 + w \bar{z} + 2 |w| |z| \\
&= (|w| + |z|)^2 \\
|w + z|
&\le |w| + |z| \\
\end{aligned}
\)
\(\blacksquare\)
Euler’s Formula#
\( \boxed{ \begin{aligned} e^{i\theta} &=\cos\theta+i\sin\theta \\ e^{i\pi}+1 &=0 \end{aligned} } \)
\( \begin{aligned} e^x &=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\frac{x^6}{6!}+\frac{x^7}{7!}+\frac{x^8}{8!}+\frac{x^9}{9!}+... &&\text{Taylor series} \\ x&=i\theta \\ e^{i\theta}&=1+(i\theta)+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!}+\frac{(i\theta)^4}{4!}+\frac{(i\theta)^5}{5!}+\frac{(i\theta)^6}{6!}+\frac{(i\theta)^7}{7!}+\frac{(i\theta)^8}{8!}+\frac{(i\theta)^9}{9!}+... \\ &=1+i\theta+\frac{(-1)\theta^2}{2!}+\frac{(-i)\theta^3}{3!}+\frac{(1)\theta^4}{4!}+\frac{(i)\theta^5}{5!}+\frac{(-1)\theta^6}{6!}+\frac{(-i)\theta^7}{7!}+\frac{(1)\theta^8}{8!}+\frac{(i)\theta^9}{9!}+... \\ &=1+i\theta-\frac{\theta^2}{2!}-\frac{i\theta^3}{3!}+\frac{\theta^4}{4!}+\frac{i\theta^5}{5!}-\frac{\theta^6}{6!}-\frac{i\theta^7}{7!}+\frac{\theta^8}{8!}+\frac{i\theta^9}{9!}-... \\ &=\left(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\frac{\theta^8}{8!}-...\right) +\left(i\theta-\frac{i\theta^3}{3!}+\frac{i\theta^5}{5!}-\frac{i\theta^7}{7!}+\frac{i\theta^9}{9!}-...\right) \\ &=\left(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+\frac{\theta^8}{8!}-...\right) +i\left(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\frac{\theta^9}{9!}-...\right) \\ &=\cos\theta+i\sin\theta \\ \theta&=\pi \\ e^{i\pi} &=\cos\pi+i\sin\pi \\ &=-1+0 \end{aligned} \)
\(i^i\)#
\( \boxed{ i^i=\,\,e^{-\frac{\pi}{2}} } \)
\( \begin{aligned} e^{i\pi} &=-1 \\ \sqrt{e^{i\pi}} &=\sqrt{-1} \\ e^{i\frac{\pi}{2}} &=i \\ (e^{i\frac{\pi}{2}})^i &=i^i \\ e^{i^2\frac{\pi}{2}}&= \\ e^{-\frac{\pi}{2}}&= \end{aligned} \)
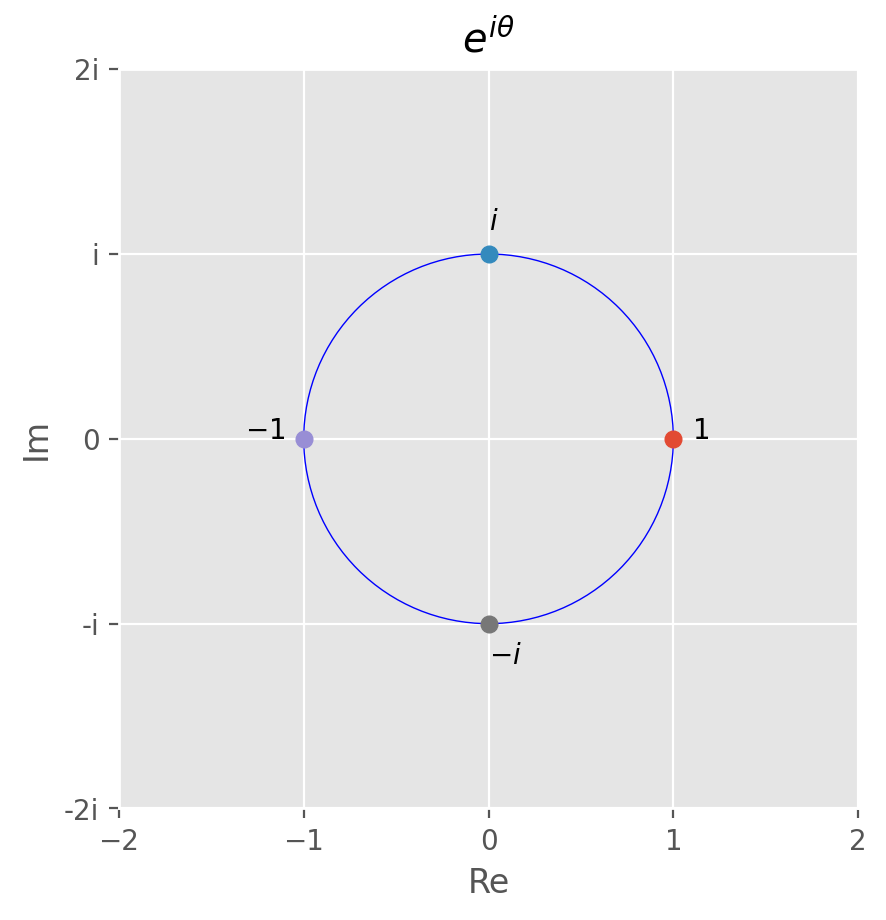
The Unit Circle in the Complex Plane#
Complex exponentials form circles!
Show code cell source
fig = plt.figure(dpi=200);
ax = plt.subplot(111,projection='rectilinear');
ax.set_aspect(1);
ax.add_patch(plt.Circle((0,0),1,edgecolor='b',facecolor='None'));
ax.scatter( 1, 0); ax.text( 1*1.1, 0, '$1$', horizontalalignment='left');
ax.scatter( 0, 1); ax.text( 0, 1*1.1, '$i$', verticalalignment='bottom');
ax.scatter(-1, 0); ax.text(-1*1.1, 0, '$-1$', horizontalalignment='right');
ax.scatter( 0,-1); ax.text( 0,-1*1.1, '$-i$', verticalalignment='top');
ax.set_xlabel('Re');
ax.set_xticks(ticks=np.arange(-2,3,1));
ax.set_xlim(-2,2);
ax.set_ylabel('Im');
ax.set_yticks(ticks=np.arange(-2,3,1),labels=['-2i','-i','0','i','2i']);
ax.set_ylim(-2,2);
ax.set_title('$e^{i\\theta}$');
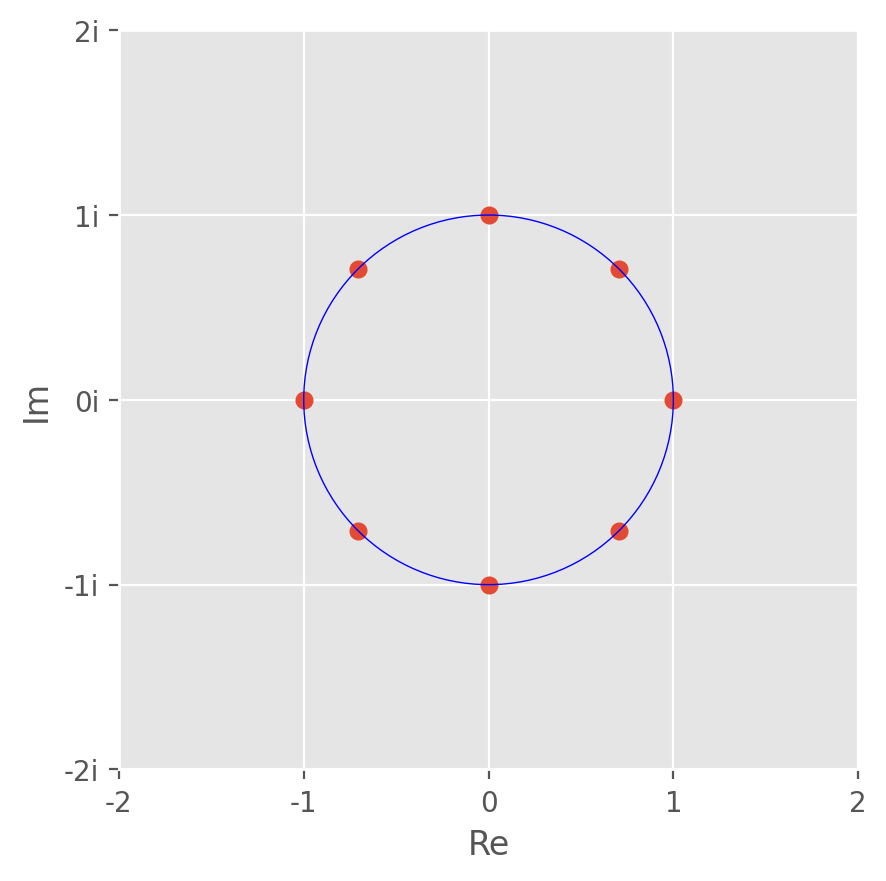
\( \begin{aligned} w^0,w^1,...,w^{n-1} \,\,\,\text{where}\,\,\, w=e^{\frac{2\pi}{n}i} \,\,\,\text{and}\,\,\, n=N \end{aligned} \)
N=8
unitCircle = {math.e ** (2*math.pi * 1j * n/N) for n in range(N)}
for i,c in enumerate(unitCircle):
display(Math(
fr'w^{i} = {c.real} + {c.imag}i'
))
pC([
unitCircle,
],-2,2,dpi=200)
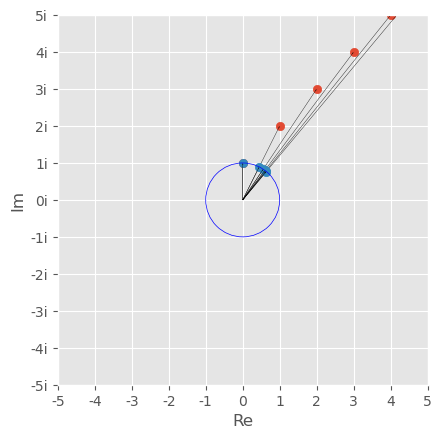
Polar Representation of Complex Numbers#
\( \boxed{ \begin{aligned} z=re^{\theta i} \,\,\,\text{where}\,\,\, r=|z| \end{aligned} } \)
zs={
0+1j,
1+2j,
2+3j,
3+4j,
4+5j,
5+6j,
}
pC([
zs,
{uC(z) for z in zs},
],-5,5,v='y')
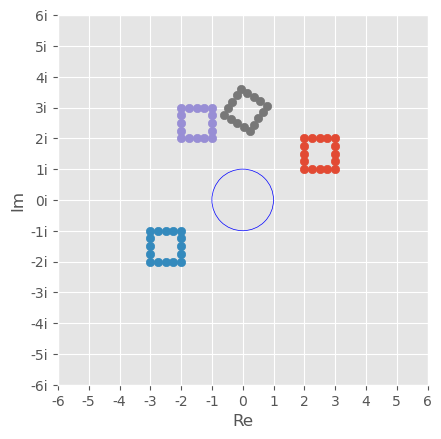
Transformations via Complex Operations#
Rotation#
To rotate a complex number \(z\) where \(\text{arg}\,\,\,z=\theta\) by \(\tau\) radians
\( \begin{aligned} re^{(\theta+\tau)i}=re^{\theta i}re^{\tau i}=ze^{\tau i} \end{aligned} \)
S={
2 +1.25j,
2 +1.50j,
2 +1.75j,
2 +2j,
2.25+2j,
2.50+2j,
2.75+2j,
3 +2j,
2 +1j,
2.25+1j,
2.5 +1j,
2.75+1j,
3 +1j,
3 +1.25j,
3 +1.50j,
3 +1.75j,
}
pC([
S,
{rotate(c,np.pi) for c in S},
{rotate(c,np.pi/2) for c in S},
{rotate(c,1) for c in S},
],-6,6,v='n')
imgRGB = mpimg.imread(fname='gandalf.png')
fig = plt.figure();
ax = plt.subplot();
ax.imshow(X=imgRGB);
ax.grid(False);
#ax.axis('off');
---------------------------------------------------------------------------
FileNotFoundError Traceback (most recent call last)
Cell In[27], line 1
----> 1 imgRGB = mpimg.imread(fname='gandalf.png')
2 fig = plt.figure();
3 ax = plt.subplot();
File ~/anaconda3/envs/ml/lib/python3.11/site-packages/matplotlib/image.py:1544, in imread(fname, format)
1537 if isinstance(fname, str) and len(parse.urlparse(fname).scheme) > 1:
1538 # Pillow doesn't handle URLs directly.
1539 raise ValueError(
1540 "Please open the URL for reading and pass the "
1541 "result to Pillow, e.g. with "
1542 "``np.array(PIL.Image.open(urllib.request.urlopen(url)))``."
1543 )
-> 1544 with img_open(fname) as image:
1545 return (_pil_png_to_float_array(image)
1546 if isinstance(image, PIL.PngImagePlugin.PngImageFile) else
1547 pil_to_array(image))
File ~/anaconda3/envs/ml/lib/python3.11/site-packages/PIL/ImageFile.py:132, in ImageFile.__init__(self, fp, filename)
128 self.decodermaxblock = MAXBLOCK
130 if is_path(fp):
131 # filename
--> 132 self.fp = open(fp, "rb")
133 self.filename = os.path.realpath(os.fspath(fp))
134 self._exclusive_fp = True
FileNotFoundError: [Errno 2] No such file or directory: 'gandalf.png'
#img=np.flip(np.dot(imgRGB,[0.2989,0.5870,0.1140]),0)
img=np.dot(imgRGB,[0.2989,0.5870,0.1140])
img.shape
(1200, 952)
fig = plt.figure();
ax = plt.subplot();
ax.imshow(X=img,cmap=mpl.pyplot.get_cmap(name='gray'),vmin=0,vmax=1);
ax.grid(False);
#ax.axis('off');
ax.set_xlim(-952,952);
ax.set_ylim(1200,-1200);
Resources#
[Y] Sanderson, Grant (3Blue1Brown). (02 Apr 2023). “Why π is in the normal distribution (beyond integral tricks)”. YouTube.
Zaczyński, Bartosz. “Simplify Complex Numbers with Python”. Real Python. Page.
Terms#
[W] Complex Analysis
[W] Complex Logarithm
[W] Complex Number
[W] Complex Plane
[W] Euler’s Formula
[W] Imaginary Unit
[W] Lacunary Value
[W] Phasor
[W] Roots of Unity
def solve1 (a,b,c):
"solves ax + b = c"
return (c-b)/a
display(
solve1(10,5,30),
solve1(10+5j,5,20),
)
2.5
(1.2-0.6j)