Polynomials#
Revised
07 Mar 2023
Real Polynomial in one variable#
DEFINITION
A real polynomial function in one variable has the form
where \(n\) is a nonnegative integer and \(a_0, a_1, a_2, ..., a_n \in \mathbb{R}\) are constants called the coefficients of the polynomial.
Degree#
If the leading coefficient \(a_n \ne 0\), then the degree of the polynomial is \(n\).
Domain#
\(\text{dom}(P(x)) = \mathbb{R}\)
General form of a linear function in one variable#
A linear function is a polynomial function of degree 1.
General form of a quadratic function in one variable#
A quadratic function is a polynomial function of degree 2.
General form of a cubic function in one variable#
A cubic function is a polynomial function of degree 3.
Polynomial Addition#
Let \(f(x) = \sum_{k = 0}^n a_k x^k\) and \(g(x) = \sum_{k = 0}^n b_k x^k\) be polynomials.
Polynomial Subtraction#
Let \(f(x) = \sum_{k = 0}^n a_k x^k\) and \(g(x) = \sum_{k = 0}^n b_k x^k\) be polynomials.
Polynomial Differentiation#
Let \(f(x) = \sum_{k = 0}^n a_k x^k\) be a polynomial.
Real Polynomial in two variables#
DEFINITION
A real polynomial in two variables has the form
where \(a_{ij} \in \mathbb{R}\) is a constant and \(m\) and \(n\) are nonnegative integers.
Degree#
If the leading coefficient \(a_{nm} \ne 0\), then the degree of the polynomial is \(n + m\).
Domain#
\(\text{dom}(P(x)) = \mathbb{R}^2\)
General form of a linear function in two variables#
A linear function is a polynomial function of degree 1.
General form of a quadratic function in two variables#
A quadratic function is a polynomial function of degree 2.
General form of a cubic function in two variables#
A cubic function is a polynomial function of degree 3.
Real Polynomial in several variables#
DEFINITION
A real polynomial in k variables has the form
Degree#
If the leading coefficient \(a_{n_1...n_k} \ne 0\), then the degree of the polynomial is \(\sum n_i\).
Domain#
\(\text{dom}(P(x)) = \mathbb{R}^k\)
General polynomial in one variable#
A function \(P : \mathbf{F} \rightarrow \mathbf{F}\) is called a polynomial with coefficients in a field \(\mathbf{F}\) if there exist \(a_0, ..., a_n \in \mathbf{F}\) such that \(P(x) = a_n x^n + ... + a_2 x^2 + a_1 x + a_0\) for all \(x \in \mathbf{F}\).
Claim
Let \(a_0, ..., a_n \in \mathbf{F}\).
If \(a_n x^n + ... + a_2 x^2 + a_1 x + a_0 = 0\) for all \(x \in \mathbf{F}\), then \(a_0 = ... = a_n = 0\) (If a polynomial is the zero function, then all coefficients are 0.)
Proof by Contrapositive
If not all the coefficients are 0, then \(a_n x^n + ... + a_2 x^2 + a_1 x + a_0 \ne 0\).
Let
\(
\begin{align}
\frac{|a_0| + |a_1| + ... + |a_{n - 1}|}{|a_n|} + 1 &= x & \text{note that}\, x \ge 1 \,\text{and}\, x^j \le x^{n - 1} \,\text{for}\, j = 0, 1, ..., n - 1 \\
|a_0| + |a_1| + ... + |a_{n - 1}| &= |a_n|(x - 1) \\
|a_0| + |a_1| + ... + |a_{n - 1}| &\lt |a_n|x \\
(|a_0| + |a_1| + ... + |a_{n - 1}|)x^{n - 1} &\lt |a_n x^n| \\
|a_0 + a_1 x + ... + a_{n - 1} x^{n - 1}| \le (|a_0| + |a_1| + ... + |a_{n - 1}|) x^{n - 1} &\lt |a_n x^n| \\
|a_0 + a_1 x + ... + a_{n - 1} x^{n - 1}| &\lt |a_n x^n| \\
a_0 + a_1 x + ... + a_{n - 1} x^{n - 1} &\ne -a_n x^n \\
a_0 + a_1 x + ... + a_{n - 1} x^{n - 1} + a_n x^n &\ne 0 \\
\end{align}
\)
\(\blacksquare\)
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-pastel')
plt.rcParams['figure.figsize'] = (10, 6)
from itertools import zip_longest
---------------------------------------------------------------------------
FileNotFoundError Traceback (most recent call last)
File ~/anaconda3/envs/ml/lib/python3.11/site-packages/matplotlib/style/core.py:137, in use(style)
136 try:
--> 137 style = _rc_params_in_file(style)
138 except OSError as err:
File ~/anaconda3/envs/ml/lib/python3.11/site-packages/matplotlib/__init__.py:866, in _rc_params_in_file(fname, transform, fail_on_error)
865 rc_temp = {}
--> 866 with _open_file_or_url(fname) as fd:
867 try:
File ~/anaconda3/envs/ml/lib/python3.11/contextlib.py:137, in _GeneratorContextManager.__enter__(self)
136 try:
--> 137 return next(self.gen)
138 except StopIteration:
File ~/anaconda3/envs/ml/lib/python3.11/site-packages/matplotlib/__init__.py:843, in _open_file_or_url(fname)
842 fname = os.path.expanduser(fname)
--> 843 with open(fname, encoding='utf-8') as f:
844 yield f
FileNotFoundError: [Errno 2] No such file or directory: 'seaborn-pastel'
The above exception was the direct cause of the following exception:
OSError Traceback (most recent call last)
Cell In[1], line 3
1 import numpy as np
2 import matplotlib.pyplot as plt
----> 3 plt.style.use('seaborn-pastel')
4 plt.rcParams['figure.figsize'] = (10, 6)
6 from itertools import zip_longest
File ~/anaconda3/envs/ml/lib/python3.11/site-packages/matplotlib/style/core.py:139, in use(style)
137 style = _rc_params_in_file(style)
138 except OSError as err:
--> 139 raise OSError(
140 f"{style!r} is not a valid package style, path of style "
141 f"file, URL of style file, or library style name (library "
142 f"styles are listed in `style.available`)") from err
143 filtered = {}
144 for k in style: # don't trigger RcParams.__getitem__('backend')
OSError: 'seaborn-pastel' is not a valid package style, path of style file, URL of style file, or library style name (library styles are listed in `style.available`)
class Polynomial:
def __init__ (self, *coefficients):
self.coefficients = list(coefficients)
def __repr__ (self):
return f"Polynomial {str(tuple(self.coefficients))}"
def __str__ (self):
def x_expr (degree):
if degree == 0:
out = ''
elif degree == 1:
out = 'x'
else:
out = f'x^{str(degree)}'
return out
degree = len(self.coefficients) - 1
out = ''
for i in range(len(self.coefficients)):
coef = self.coefficients[i]
if abs(coef) == 1 and i < degree:
out += f"{'+' if coef > 0 else '-'}{x_expr(degree - i)}"
elif coef != 0:
out += f"{coef:+g}{x_expr(degree - i)}"
return out.lstrip('+')
def __call__ (self, x):
#return [0 * x + coef for coef in self.coefficients]
return sum([coef * x ** index for index, coef in enumerate(self.coefficients[::-1])])
def degree (self):
return len(self.coefficients)
def __add__ (self, other):
P1 = self.coefficients[::-1]
P2 = other.coefficients[::-1]
return self.__class__(*[sum(t) for t in zip_longest(P1, P2, fillvalue=0)][::-1])
def __sub__ (self, other):
P1 = self.coefficients[::-1]
P2 = other.coefficients[::-1]
return self.__class__(*[t1 - t2 for t1, t2 in zip_longest(P1, P2, fillvalue=0)][::-1])
def derivative (self):
derived_coefs = []
exponent = len(self.coefficients) - 1
for i in range(len(self.coefficients) - 1):
derived_coefs.append(self.coefficients[i] * exponent)
exponent -= 1
return self.__class__(*derived_coefs)
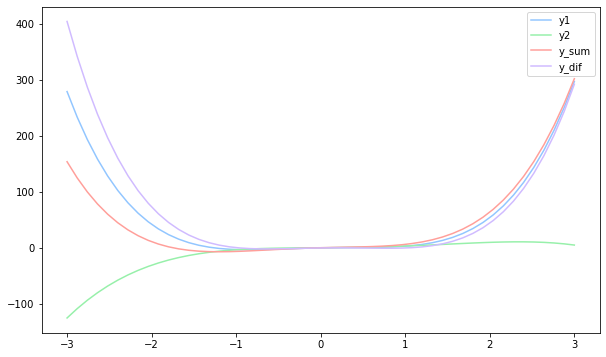
p1 = Polynomial(4, 0, -4, 3, 0)
p2 = Polynomial(-0.8, 2.3, 0.5, 1, 0.2)
p_sum = p1 + p2
p_dif = p1 - p2
x = np.linspace(-3, 3, 51)
y1 = p1(x)
y2 = p2(x)
y_sum = p_sum(x)
y_dif = p_dif(x)
plt.plot(x, y1, label='y1')
plt.plot(x, y2, label='y2')
plt.plot(x, y_sum, label='y_sum')
plt.plot(x, y_dif, label='y_dif')
plt.legend();
n = 5
display(
(n + 1)**2,
(n + 1)**2 - sum(range(n + 1)),
sum(range(n + 2)),
sum(range(n + 1)),
)
36
21
21
15
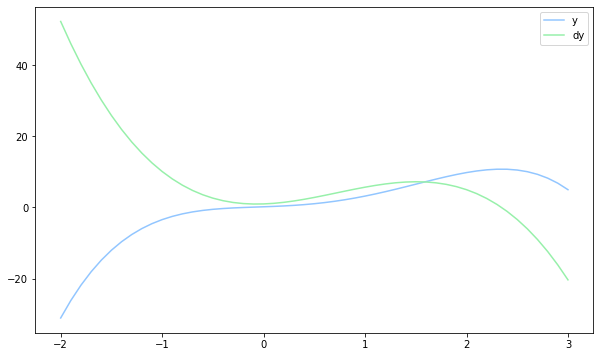
p = Polynomial(-0.8, 2.3, 0.5, 1, 0.2)
dp = p.derivative()
x = np.linspace(-2, 3, 51)
y = p(x)
df = dp(x)
plt.plot(x, y, label='y')
plt.plot(x, df, label='dy')
plt.legend();
print(p)
print(dp)
for count, poly in enumerate([p]):
print(f'$p_{count} = {str(poly)}$')
$p_0 = -0.8x^4+2.3x^3+0.5x^2+x+0.2$
Figures#
[W] François Viète (1540-1603)
Terms#
[W] list of polynomial topics
[W] Algebraic Equation (Polynomial Equation)
[W] Binomial
[W] Characteristic Polynomial
[W] Coefficient
[W] Constant Term
[W] Degree
[W] Exponential Polynomial
[W] Factor Theorem
[W] Factorization of Polynomials
[W] Gauss’s Lemma
[W] Geometric Properties of Polynomial Roots
[W] Greatest Common Divisor Polynomial
[W] Homogeneous Polynomial
[W] Horner’s Method
[W] Irreducible Polynomial
[W] Laurent Polynomial
[W] Like Terms
[W] Little Bézout’s Theorem (Polynomial Remainder Theorem)
[W] Matrix Polynomial
[W] Monic Polynomial
[W] Monomial
[W] Orthogonal Polynomials
[W] Polynomial
[W] Polynomial Equation (Algebraic Equation)
[W] Polynomial Evaluation
[W] Polynomial Long Division
[W] Polynomial Remainder Theorem (Little Bézout’s Theorem)
[W] Primitive Part of a polynomial
[W] Root
[W] Root-Finding Algorithm
[W] Ruffini’s Rule
[W] Sparse Polynomial
[W] Synthetic Division
[W] System of Polynomial Equations
[W] Trigonometric Polynomial
[W] Trinomial
[W] Vieta’s Formulas