Derivatives

Derivatives#

Revised

14 Jun 2023

Programming Environment#

Hide code cell source 
import numpy             as np
import pandas            as pd
import matplotlib        as mpl
import matplotlib.pyplot as plt
from   matplotlib           import gridspec
from   mpl_toolkits.mplot3d import axes3d
from   ipywidgets           import interactive
plt.style.use('ggplot');

import sympy as smp
from   sympy import *

import plotly
import plotly.figure_factory as ff
import plotly.graph_objects  as go

from IPython.display import display, Math

from   datetime import datetime as d
import locale                   as l
import platform                 as p
import sys                      as s

pad = 20
print(f"{'Executed'.upper():<{pad}}: {d.now()}")
print()
print(f"{'Platform'        :<{pad}}: "
      f"{p.mac_ver()[0]} | "
      f"{p.system()} | "
      f"{p.release()} | "
      f"{p.machine()}")
print(f"{''                :<{pad}}: {l.getpreferredencoding()}")
print()
print(f"{'Python'          :<{pad}}: {s.version}")
print(f"{''                :<{pad}}: {s.version_info}")
print(f"{''                :<{pad}}: {p.python_implementation()}")
print()
print(f"{'Matplotlib'      :<{pad}}: {mpl   .__version__}")
print(f"{'NumPy'           :<{pad}}: {np    .__version__}")
print(f"{'Pandas'          :<{pad}}: {pd    .__version__}")
print(f"{'Plotly'          :<{pad}}: {plotly.__version__}")
print(f"{'SymPy'           :<{pad}}: {smp   .__version__}")

EXECUTED            : 2024-05-21 15:45:37.858861

Platform            : 14.4.1 | Darwin | 23.4.0 | arm64
                    : UTF-8

Python              : 3.11.9 | packaged by conda-forge | (main, Apr 19 2024, 18:34:54) [Clang 16.0.6 ]
                    : sys.version_info(major=3, minor=11, micro=9, releaselevel='final', serial=0)
                    : CPython

Matplotlib          : 3.8.4
NumPy               : 1.26.4
Pandas              : 2.2.2
Plotly              : 5.21.0
SymPy               : 1.12

\(\begin{aligned}\frac{d}{dx} \left( \frac{1 + \sin(x)}{1 - \cos(x)} \right)^2\end{aligned}\)#

\( \begin{aligned} \frac{d}{dx} \left( \frac{1 + \sin(x)}{1 - \cos(x)} \right)^2 \end{aligned} \)

x = smp.symbols('x')

smp.diff(
  ((1 + smp.sin(x)) / (1 - smp.cos(x)))**2,
  x,
  1, # first derivative
)
\[\displaystyle \frac{2 \left(\sin{\left(x \right)} + 1\right) \cos{\left(x \right)}}{\left(1 - \cos{\left(x \right)}\right)^{2}} - \frac{2 \left(\sin{\left(x \right)} + 1\right)^{2} \sin{\left(x \right)}}{\left(1 - \cos{\left(x \right)}\right)^{3}}\]

\(\begin{aligned}\frac{d}{dx} \left( \frac{y + \sin(x)}{1 - \cos(x)} \right)^2\end{aligned}\)#

\( \begin{aligned} \frac{d}{dx} \left( \frac{y + \sin(x)}{1 - \cos(x)} \right)^2 \end{aligned} \)

x, y = smp.symbols('x y')

smp.diff(((y + smp.sin(x)) / (1 - smp.cos(x)))**2, x, 1)
\[\displaystyle \frac{2 \left(y + \sin{\left(x \right)}\right) \cos{\left(x \right)}}{\left(1 - \cos{\left(x \right)}\right)^{2}} - \frac{2 \left(y + \sin{\left(x \right)}\right)^{2} \sin{\left(x \right)}}{\left(1 - \cos{\left(x \right)}\right)^{3}}\]

\(\begin{aligned}\frac{d}{dx} (\log_5(x))^\frac{x}{2}\end{aligned}\)#

\( \begin{aligned} \frac{d}{dx} (\log_5(x))^\frac{x}{2} \end{aligned} \)

x = smp.symbols('x')

smp.diff(smp.log(x, 5)**(x/2), x, 1)
\[\displaystyle \left(\frac{\log{\left(x \right)}}{\log{\left(5 \right)}}\right)^{\frac{x}{2}} \left(\frac{\log{\left(\frac{\log{\left(x \right)}}{\log{\left(5 \right)}} \right)}}{2} + \frac{1}{2 \log{\left(x \right)}}\right)\]

\(\begin{aligned}\frac{d}{dx} f(x + g(x))\end{aligned}\)#

\( \begin{aligned} \frac{d}{dx} f(x + g(x)) \end{aligned} \)

x    = smp.symbols('x')
f, g = smp.symbols('f g', cls=smp.Function)

g = g(x)
f = f(x + g)

smp.diff(f, x, 1)
\[\displaystyle \left(\frac{d}{d x} g{\left(x \right)} + 1\right) \left. \frac{d}{d \xi_{1}} f{\left(\xi_{1} \right)} \right|_{\substack{ \xi_{1}=x + g{\left(x \right)} }}\]

Trigonometric Functions#

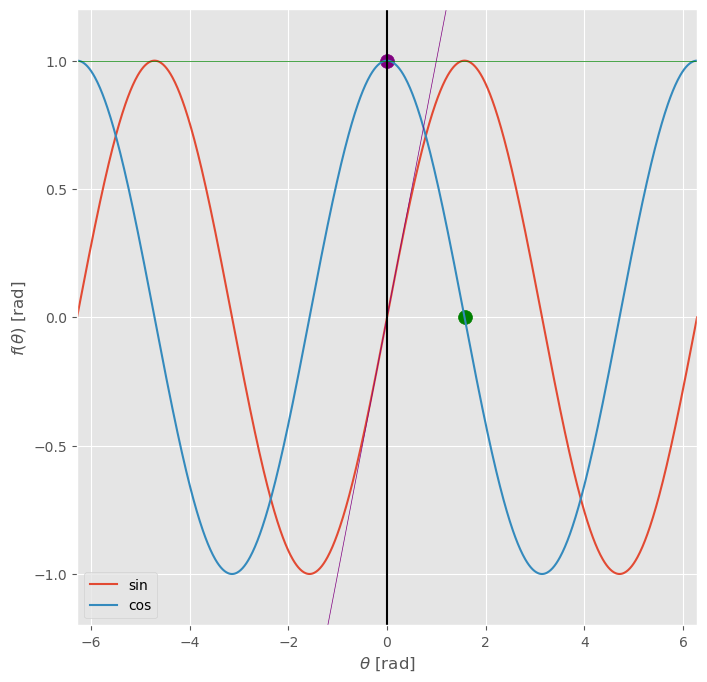
\(\begin{aligned}\frac{d}{d\theta}\sin\theta=\cos\theta\end{aligned}\)#

\( \begin{aligned} \frac{d}{d\theta}\sin\theta\,[\text{rad}]=\cos\theta\,[\text{rad}] \end{aligned} \)

\( \begin{aligned} \frac{\Delta y}{\Delta x} &=\frac{y_2-y_1}{x_2-x_1} =\frac{\sin(x+\Delta x)-\sin x}{x+\Delta x-x} =\frac{\sin x\cos\Delta x+\cos x\sin\Delta x-\sin x}{\Delta x} =\frac{\sin x\cos\Delta x-\sin x}{\Delta x}+\frac{\cos x\sin\Delta x}{\Delta x} \\ \frac{dy}{dx} =\lim_{\Delta x\to0}\frac{\Delta y}{\Delta x} &=\sin x\lim_{\Delta x\to0}\frac{\cos\Delta x-1}{\Delta x}+\cos x\lim_{\Delta x\to0}\frac{\sin\Delta x}{\Delta x} =\cos x \end{aligned} \)

Hide code cell source 
t =np.linspace(-2*np.pi,2*np.pi,1001)
f =np.sin(t)
df=np.cos(t)

fig=plt.figure(figsize=(8,8));
ax =plt.subplot();
ax.plot(t, f,label='sin');
ax.plot(t,df,label='cos');
ax.scatter(0,1,color='purple',s=100);
ax.plot(t,t,color='purple',linewidth=0.5);
ax.scatter(np.pi/2,0,color='green',s=100);
ax.plot(t,np.ones(1001),color='green',linewidth=0.5);
ax.axvline(0,color='k');
ax.set_xlim(-2*np.pi,2*np.pi);
ax.set_xlabel('$\\theta$ [rad]');
ax.set_ylim(-1.2,1.2)
ax.set_ylabel('$f(\\theta)$ [rad]');
ax.legend();
../../../_images/1dc3e88afa275b3831de677994fc7d68c723112ba81ce123d6c9d4c7d81032e4.png

To Review#

Finite Difference

\( f(x+b)-f(x+a) \)

Difference Quotient

\( \begin{aligned} \frac{f(x+b)-f(x+a)}{b-a} \end{aligned} \)

Difference Operator

\( \Delta:f\rightarrow\Delta[f] \)

Newton’s Difference Quotient, or a first-order divided difference

\( \begin{aligned} \frac{f(x+h)-f(x)}{h} \end{aligned} \)

Definition of the Derivative of \(f\) at \(x\)

\( \begin{aligned} f'(x) \overset{\text{def}}{=} \underset{h\rightarrow0}{\lim}\frac{f(x+h)-f(x)}{h} \end{aligned} \)

Terms#

  • [w] Antiderivative

  • [w] Antidifference (Indefinite Sum)

  • [w] Derivative

  • [w] Difference Operator

  • [w] Difference Quotient

  • [w] Differentiable Function

  • [w] Discrete Calculus

  • [w] Divided Difference

  • [w] Finite Difference

  • [w] Functional Equation

  • [w] Indefinite Sum (Antidifference)

  • [w] Infinitesimal

  • [w] Instant

  • [w] Rate

  • [w] Recurrence Relation

  • [w] Semi Differentiability

  • [w] Symmetric Derivative

  • [w] Time-Scale Calculus

Bibliography#

  • [Y] Mr. P Solver. (26 May 2021). “1st Year Calculus, But in PYTHON”. YouTube.

Contents